Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét hình a.Cạnh lớn trong hai cạnh còn lại là cạnh đối diện với góc 45o. Gọi cạnh đó là x. Ta có
Xét hình b. Cạnh lớn trong hai cạnh là cạnh kề với góc 45o. Gọi cạnh đó là y. Ta có:
Xét hình a.Cạnh lớn trong hai cạnh còn lại là cạnh đối diện với góc 45o. Gọi cạnh đó là x. Ta có
Xét hình b. Cạnh lớn trong hai cạnh là cạnh kề với góc 45o. Gọi cạnh đó là y. Ta có:

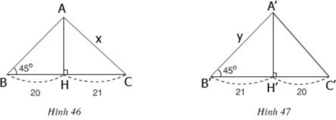
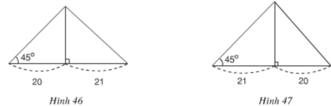
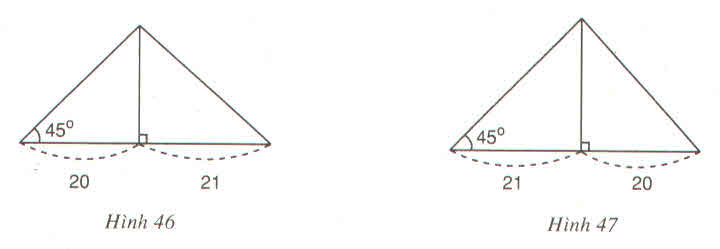
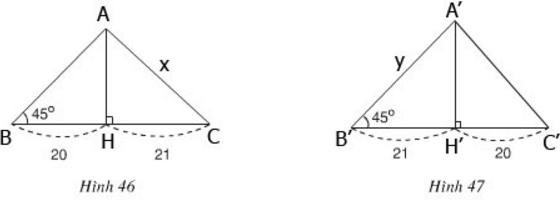
- Trường hợp hình 46: cạnh lớn trong hai cạnh còn lại được kí hiệu là x.
ΔHAB cân vì có ∠ B = 45 °
=> HA = HB = 20
Áp dụng định lí Pitago trong ΔHAC có:
x 2 = A C 2 = H A 2 + H C 2 = 20 2 + 21 2 = 841
=> x = 29 hay độ dài cạnh lớn trong hai cạnh còn lại là 29.
- Trường hợp hình 47: cạnh lớn trong hai cạnh còn lại được kí hiệu là y.
ΔH'A'B' cân vì có ∠ B ' = 45 °
=> H'A' = H'B' = 21
Áp dụng định lí Pitago trong ΔH'A'B' có:
y 2 = A ' B ' 2 = H ' A ' 2 + H ' B ' 2 = 21 2 + 21 2 = 2 . 21 2
=> y = 21√2 ≈ 29,7 hay độ dài cạnh lớn trong hai cạnh còn lại là 29,7.


Giả sử ABCD là hình thang cân thỏa điều kiện đề bài.
Hạ đường cao AH, BK xuống BC
Ta tính được DH = \(\frac{CD-AB}{2}=18\left(cm\right)\)
\(\Rightarrow HC=CD-DH=32\left(cm\right)\)
\(\Rightarrow AH=\sqrt{DH.HC}=24\left(cm\right)\)
Từ đó tính được diện tích hình thang ABCD là : \(768cm^2\)
vẽ đườg cao AH&BK.táco:
Tamgiác AHD=támgiacBKC(ccạnh huynề-góc nhọn)
-->DH=KC mà:DC=DH+HK+KC ---->DC=2DH+HK----->DH=(DC-HK):2
mà HK=AB(ABKH là hcn)
dođo:DH=(DC-AB):2=(50-14):2=18
--->HC=32
tamgiác AHD có H^=90dộ theo HTL có:AH^2= DHxHC=18x32=576
--->AH=24
Rùi đó bạn tự tính S hình thang nha!

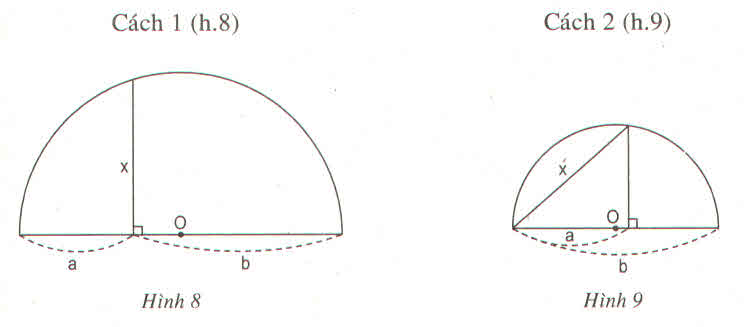
Cách 1: Đặt tên các đoạn thẳng như hình bên.
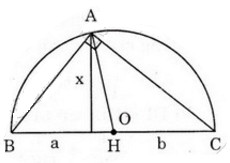
Ta có:
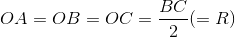 .
.
Suy ra 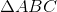 vuông tại A.
vuông tại A.
Áp dụng hệ thức 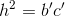 ta có:
ta có: 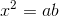
Cách 2:
Cũng chứng minh 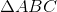 vuông như cách 1.
vuông như cách 1.
Áp dụng hệ thức 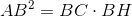 ta được
ta được 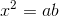 .
.

Đặt \(\frac{AB}{BC}=\frac{3}{5}=x\Rightarrow AB=3x;BC=5x\)
Tam giác ABC vuông tại A, theo py ta go:
\(AB^2+AC^2=BC^2\Rightarrow9x^2+144=25x^2\Rightarrow16x^2=144\Leftrightarrow x^2=9\)
=> X = 3 ; AB = 3x = 3.3=9 ; BC= 5x = 5.3 = 15
TAm giac ABC vuông tại A theo hệ thức lượng
AH.BC = AB.AC => AH= (AB.AC)/BC = (9.12)/15 = 7,2cm
AB^2 = BC . BH => BH = AB^2 /BC = 9^2/15 = 5,4
=> HC = BC - HB = 15 - 5,4 = 9,6cm
VẬY AH = 7,2 ; BH = 5,4;CH = 9,6

Ta có : \(OB^2+OE^2=6,25\)
Và : \(OD^2+OC^2=25\)
Mà: \(OD=\frac{1}{2}OB\)
\(OC=2OE\)
\(\Rightarrow\text{OE}=2,5\)
\(\Rightarrow OB=0\)
\(\Rightarrow BC=5\)
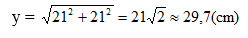
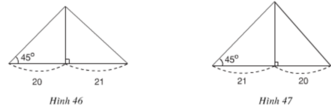


- Trường hợp hình 46: cạnh lớn trong hai cạnh còn lại được kí hiệu là x.
ΔHAB cân vì có ∠B = 45o
=> HA = HB = 20
Áp dụng định lí Pitago trong ΔHAC có:
x2 = AC2 = HA2 + HC2 = 202 + 212 = 841
=> x = 29 hay độ dài cạnh lớn trong hai cạnh còn lại là 29.
- Trường hợp hình 47: cạnh lớn trong hai cạnh còn lại được kí hiệu là y.
ΔH'A'B' cân vì có ∠B' = 45o
=> H'A' = H'B' = 21
Áp dụng định lí Pitago trong ΔH'A'B' có:
y2 = A'B'2 = H'A'2 + H'B'2 = 212 + 212 = 2.212
=> y = 21√2 ≈ 29,7 hay độ dài cạnh lớn trong hai cạnh còn lại là 29,7.