Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

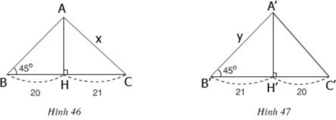
- Trường hợp hình 46: cạnh lớn trong hai cạnh còn lại được kí hiệu là x.
ΔHAB cân vì có ∠ B = 45 °
=> HA = HB = 20
Áp dụng định lí Pitago trong ΔHAC có:
x 2 = A C 2 = H A 2 + H C 2 = 20 2 + 21 2 = 841
=> x = 29 hay độ dài cạnh lớn trong hai cạnh còn lại là 29.
- Trường hợp hình 47: cạnh lớn trong hai cạnh còn lại được kí hiệu là y.
ΔH'A'B' cân vì có ∠ B ' = 45 °
=> H'A' = H'B' = 21
Áp dụng định lí Pitago trong ΔH'A'B' có:
y 2 = A ' B ' 2 = H ' A ' 2 + H ' B ' 2 = 21 2 + 21 2 = 2 . 21 2
=> y = 21√2 ≈ 29,7 hay độ dài cạnh lớn trong hai cạnh còn lại là 29,7.

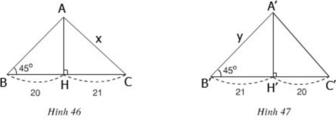
- Trường hợp hình 46: cạnh lớn trong hai cạnh còn lại được kí hiệu là x.
ΔHAB cân vì có ∠B = 45o
=> HA = HB = 20
Áp dụng định lí Pitago trong ΔHAC có:
x2 = AC2 = HA2 + HC2 = 202 + 212 = 841
=> x = 29 hay độ dài cạnh lớn trong hai cạnh còn lại là 29.
- Trường hợp hình 47: cạnh lớn trong hai cạnh còn lại được kí hiệu là y.
ΔH'A'B' cân vì có ∠B' = 45o
=> H'A' = H'B' = 21
Áp dụng định lí Pitago trong ΔH'A'B' có:
y2 = A'B'2 = H'A'2 + H'B'2 = 212 + 212 = 2.212
=> y = 21√2 ≈ 29,7 hay độ dài cạnh lớn trong hai cạnh còn lại là 29,7.

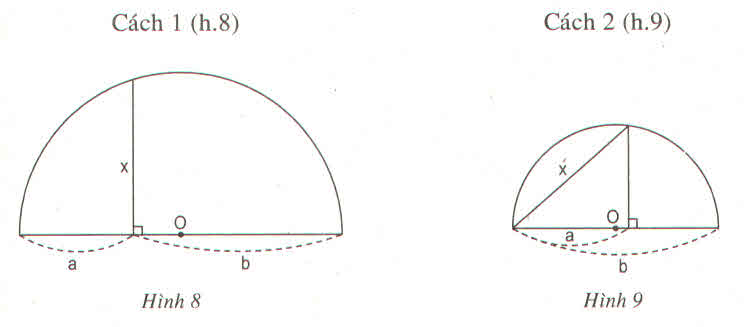
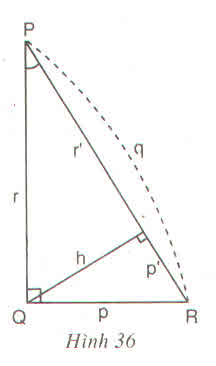
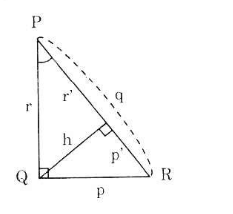
Cách 1: Đặt tên các đoạn thẳng như hình bên.
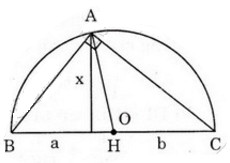
Ta có:
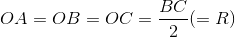 .
.
Suy ra 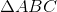 vuông tại A.
vuông tại A.
Áp dụng hệ thức 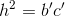 ta có:
ta có: 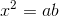
Cách 2:
Cũng chứng minh 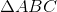 vuông như cách 1.
vuông như cách 1.
Áp dụng hệ thức 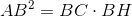 ta được
ta được 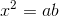 .
.

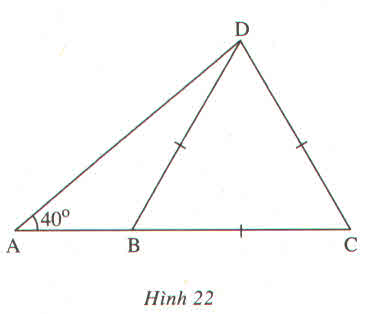
b: XétΔADE vuông tại E có \(AE=AD\cdot\cos A\)
nên AE=5,16(cm)
AB=AE-BE=2,66(cm)

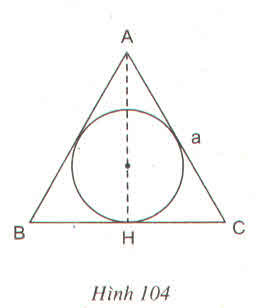
đặt MA= x (cm)
tam giác ABC cân nên : 12-x
diện tích hình bình hành MNCP là : MP.MA = (12-x)x
diện tích bằng 32cm vuông , nê ta có phương trình:
x^2 -12x +32 = 0
giải pt ta được x1= 4 , x2 =8
vậy M cách A là 4cm hoặc 8cm.
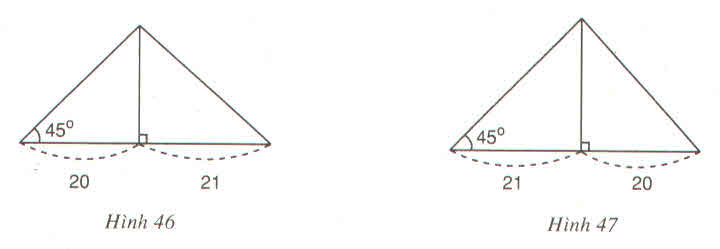
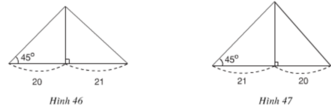
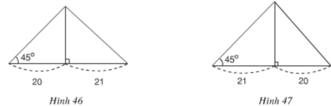



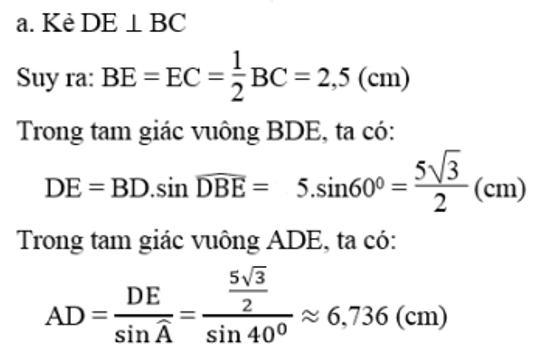





Xét hình a.Cạnh lớn trong hai cạnh còn lại là cạnh đối diện với góc 45o. Gọi cạnh đó là x. Ta có
Xét hình b. Cạnh lớn trong hai cạnh là cạnh kề với góc 45o. Gọi cạnh đó là y. Ta có:
Xét hình a.Cạnh lớn trong hai cạnh còn lại là cạnh đối diện với góc 45o. Gọi cạnh đó là x. Ta có
Xét hình b. Cạnh lớn trong hai cạnh là cạnh kề với góc 45o. Gọi cạnh đó là y. Ta có: