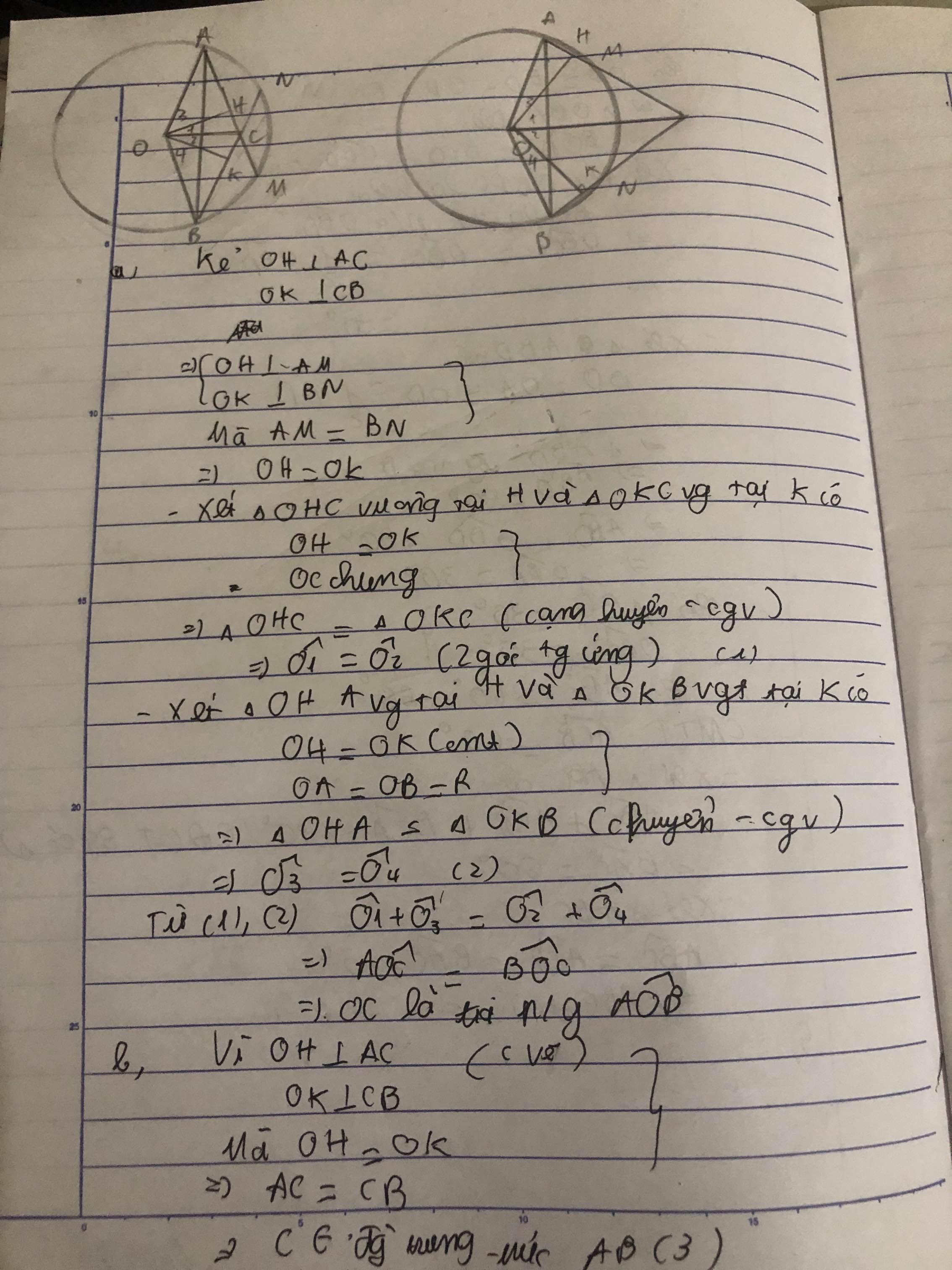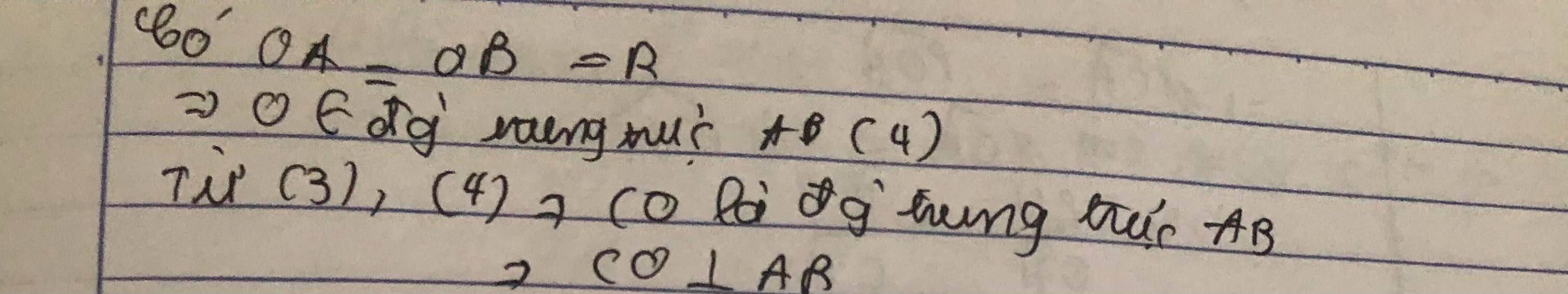Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

góc COB=40+110=150 độ
=>sđ cung nhỏ BC=150 độ
sđ cung lớn BC=360-150=210 độ

Theo giả thiết: Vì số đo cung \(\stackrel\frown{AC}=40^o\)
\(\Rightarrow\) Góc ở tâm \(\widehat{AOC}=40^o\)
Trường hợp 1: C thuộc cung nhỏ \(\stackrel\frown{AB}\)
- Số đo góc ở tâm \(\widehat{BOC}=\widehat{AOB}-\widehat{AOC}=110^o-40^o=70^o\)
Do vậy:
- Số đo cung nhỏ \(\stackrel\frown{BC}=70^o\)
- Số đo cung lớn \(\stackrel\frown{BC}=360^o-70^o=290^o\)
Trường hợp 2: C thuộc cung lớn \(\stackrel\frown{BC}\)
- Số đo góc ở tâm \(\widehat{BOC}=\widehat{BOA}+\widehat{AOC}=110^o+40^o=150^o\)
Do vậy:
- Số đo cung nhỏ \(\stackrel\frown{BC}=150^o\)
- Số đo cung lớn \(\stackrel\frown{BC}=360^o-150^o=210^o\)

a) Điểm C nằm trên cung nhỏ AB ( hình a)
Số đo cung nhỏ BC = 100º – 45º = 55º
Số đo cung lớn BC = 360º – 55º = 305º
b) Điểm C nằm trên cung lớn AB (hình b)
Số đo cung nhỏ BC = 100º + 45º = 145º
Số đo cung lớn BC = 360º – 145º = 215º

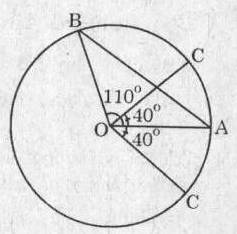
a) Kẻ OP ⊥ AM, OQ ⊥ BN
Ta có: AM = BN (Giả thiết)
Suy ra: OP = OQ (hai dây bằng nhau cách đều tâm)
Xét hai tam giác OCP và OCQ, ta có:
Góc OPC= góc OQC=90∘
OC chung
OP = OQ (chứng minh trên)
Suy ra: ∆OCP = ∆OCQ (cạnh huyền, cạnh góc vuông)
Góc O1= góc O2
Xét hai tam giác OAP và OBQ, ta có:
Góc OPA= góc OQB=90∘
OA = OB
OP = OQ ( chứng minh trên)
Suy ra: ∆OAP = ∆OBQ (cạnh huyền, cạnh góc vuông)
Góc O3= Góc O4
Suy ra: Góc O1+góc O3= Góc O2+ góc O4 hay Góc AOC= Góc BOC
Vậy OC là tia phân giác của Góc AOB
b) Tam giác OAB cân tại O có OC là tia phân giác nên OC đồng thời cũng là đường cao ( tính chất tam giác cân).
Suy ra: OC ⊥ AB.

A B C O D E K M F T y x
c) Gọi T là giao điểm thứ hai của FD với đường tròn (O). Ta c/m EO đi qua T.
Ta có: ^ADM = ^DAC + ^DCA = ^BAC/2 + ^ACB = ^BAD + ^MAB = ^MAD => \(\Delta\)DAM cân tại M => MA=MD
Lại có: MA và MF là 2 tiếp tuyến của (O) nên MA=MF. Do đó: MD=MF => \(\Delta\)MDF cân tại M (đpcm).
Dễ thấy: \(\Delta\)MAB ~ \(\Delta\)MCA (g.g) và \(\Delta\)MFB ~ \(\Delta\)MCF (g.g)
=> \(\frac{MA}{MC}=\frac{MF}{MC}=\frac{AB}{AC}=\frac{BD}{CD}=\frac{FB}{FC}\) => FD là tia phân giác ^BFC (1)
Kẻ tia đối Fy của FB => ^EFy = ^ECB = ^EBC = ^EFC => FE là phân giác ^CFy (2)
Từ (1) và (2) suy ra: FD vuông góc với FE (Vì ^BFC + ^CFy = 1800) hay ^EFT = 900
=> ET là đường kính của (O) => ET trùng với OE => OE đi qua T => ĐPCM.
d) Áp dụng ĐL Ptolemy có tứ giác BFCT nội tiếp có: BF.CT + CF.BT = BC.FT
=> CT.(BF+CF) = BC.FT => \(BF+CF=\frac{BC.FT}{CT}\le\frac{BC.ET}{CT}=\frac{2CK.ET}{CT}=2EC=2BE\)
Dấu "=" xảy ra khi F trùng với E <=> MF vuông góc OE <=> MF // BC => M không nằm trên BC (mâu thuẫn)
=> Không có dấu "=" => BF+CF < 2BE (đpcm).