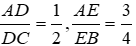Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

áp dụng tính chất đường phân giác ta có : AD/DC=AB/BC hay AD/AB=DC/BC
theo tính chất của dãy tỉ số bằng nhau, ta co: AD/AB=DC/BC =( AD+DC)/ (AB+BC)=6/10=3/5
VẬY AD = 3/5 x AB=3/5 x 6 =18/5 cm

a: BC=10cm
b: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\)
Do đó: ΔHAB∼ΔHCA

a,Xét tam giác DAC và tam giác EBC ta có:
\(\widehat{BEC}=\widehat{ADC}=90^0\)
C chung
tam giác DAC đồng dạng tam giác EBC
b, AD là đường cao vừa là đường phân giác
BD = DC
DC = \(\dfrac{BC}{2}\) =\(\dfrac{6}{3}=2\)
Vì tam giác DAC đồng dạng tam giác EBC suy ra \(\dfrac{AC}{BC}=\dfrac{DC}{EC}\Leftrightarrow EC=\dfrac{DC.BC}{AC}=\dfrac{3.6}{9}=2\)
c, vì đường cao BE,CF nên \(\widehat{BEC}=\widehat{CFB}=90^o\)
Xét tam giác BEC và tam giác CFB có
BC chung
\(\widehat{CBA}=\widehat{BCA}\)
tam giác BEC = tam giác CFB ( cạnh huyền góc nhọn )
CE = BF ( đpcm )
Ta có : AB = AC , CE = BF
AB = BF + AF ; AC = CE + AE
suy ra AF = AE => tam giác AEF cân tại A
\(\widehat{ÀEF}=\dfrac{180^o-\widehat{A}}{2}\) ( 1 )
tam giác ABC cân tại A suy ra \(\widehat{ACB}=\dfrac{180^o-\widehat{A}}{2}\) ( 2 )
TỪ ( 1 ) và ( 2 ) ta có \(\widehat{AEF}=\widehat{ACB}\)
suy ra EF//BC ( có cặp góc đồng vị bằng nhau )
a) Xét ΔDAC vuông tại D và ΔEBC vuông tại E có
\(\widehat{ECB}\) chung
Do đó: ΔDAC∼ΔEBC(g-g)

b: Xét ΔADB và ΔAEC có
\(\widehat{A}\) chung
\(\widehat{ABD}=\widehat{ACE}\left(=\dfrac{1}{2}\widehat{ABC}\right)\)
Do đó: ΔADB\(\sim\)ΔAEC