Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

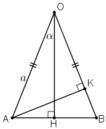
ΔAOB cân tại O nên OH là đường cao đồng thời là đường phân giác
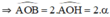
Xét ΔOAK vuông tại K có:
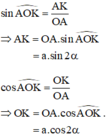

Ta có = 2α => Trong tam giác OKA có:
AK = OA.sin. => AK = a.sin2α
OK =OA.cos. => OK = a.cos2α



a) Do MN song song với Ox nên \(\alpha = \widehat {OMN} = \widehat {ONM} = \widehat {NOx'}\)
Mà \(\widehat {xON} = {180^o} - \widehat {NOx'} = {180^o} - \alpha \)
\( \Rightarrow \widehat {xON} = {180^o} - \alpha \)
b) Dễ thấy: Điểm N đối xứng với M qua trục Oy
\( \Rightarrow N( - {x_0};{y_0})\)
Lại có: điểm N biểu diễn góc \({180^o} - \alpha \)
\( \Rightarrow \left\{ \begin{array}{l}\sin ({180^o} - \alpha ) = {y_N} = {y_0}\\\cos ({180^o} - \alpha ) = {x_N} = - {x_0}\end{array} \right.\);
Mà: \(\sin \alpha = {y_0};\;\cos \alpha = {x_0}\)
\( \Rightarrow \left\{ \begin{array}{l}\sin ({180^o} - \alpha ) = \sin \alpha \;\\\cos ({180^o} - \alpha ) = - \cos \alpha \end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}\tan ({180^o} - \alpha ) = - \tan \alpha \;\\\cot ({180^o} - \alpha ) = - \cot \alpha \end{array} \right.\)

a:
2: pi/2<a<pi
=>sin a>0 và cosa<0
tan a=-2
1+tan^2a=1/cos^2a=1+4=5
=>cos^2a=1/5
=>\(cosa=-\dfrac{1}{\sqrt{5}}\)
\(sina=\sqrt{1-\dfrac{1}{5}}=\dfrac{2}{\sqrt{5}}\)
cot a=1/tan a=-1/2
3: pi<a<3/2pi
=>cosa<0; sin a<0
1+cot^2a=1/sin^2a
=>1/sin^2a=1+9=10
=>sin^2a=1/10
=>\(sina=-\dfrac{1}{\sqrt{10}}\)
\(cosa=-\dfrac{3}{\sqrt{10}}\)
tan a=1:cota=1/3
b;
tan x=-2
=>sin x=-2*cosx
\(A=\dfrac{2\cdot sinx+cosx}{cosx-3sinx}\)
\(=\dfrac{-4cosx+cosx}{cosx+6cosx}=\dfrac{-3}{7}\)
2: tan x=-2
=>sin x=-2*cosx
\(B=\dfrac{-4cosx+3cosx}{-6cosx-2cosx}=\dfrac{1}{8}\)

Áp dụng định lí cosin trong tam giác ABC ta có:
\(B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\)
\(\begin{array}{l} \Leftrightarrow B{C^2} = {c^2} + {b^2} - 2.c.b.\cos \alpha \\ \Leftrightarrow BC = \sqrt {{c^2} + {b^2} - 2bc.\cos \alpha } \end{array}\)
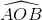 = 2α => Trong tam giác OKA có:
= 2α => Trong tam giác OKA có: => AK = a.sin2α
=> AK = a.sin2α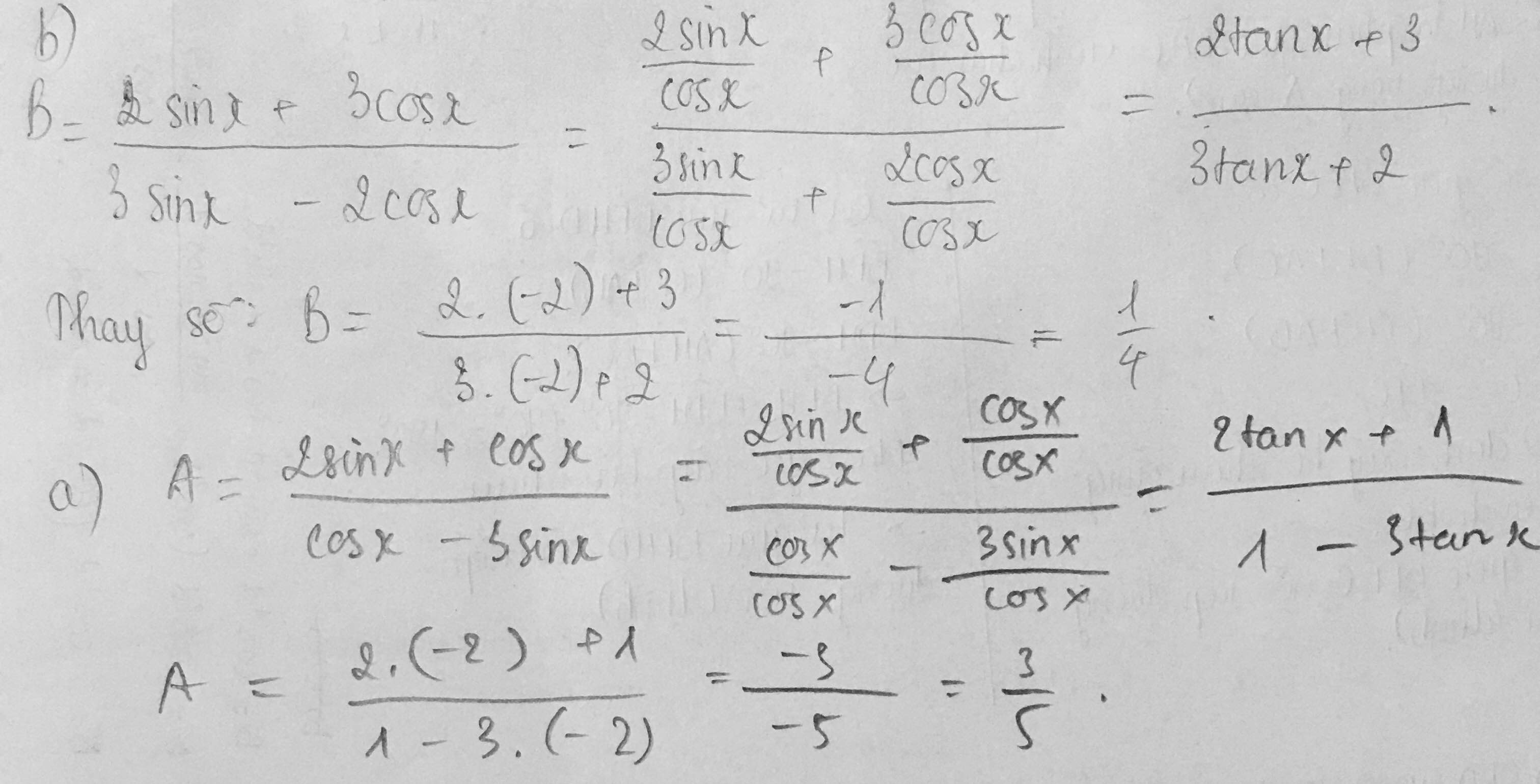
\(\widehat{O}=2\widehat{AOH}=2\alpha\)
Trong tam giác vuông AOK:
\(AK=OA.sin\widehat{O}=a.sin\left(2\alpha\right)\)
Trong tam giác vuông AOH:
\(OH=OA.cos\widehat{AOH}=a.cos\alpha\)
vậy TH góc AOH tù thì sao bạn? Không xét à?