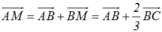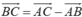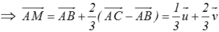cho tam giác ABC,M thuộc BC,sao cho MB=-2MC, N thuộc AC saocho NA=-NCbiểu diễn AM,BN,MNtheo u và v với u=AB,v=AC

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

TM

Tạ Minh Châu

11 tháng 10 2019

cho tam giác ABC,M thuộc BC,sao cho MB=-2MC, N thuộc AC saocho NA=-NCbiểu diễn AM,BN,MNtheo u và v với u=AB,v=AC

#Toán lớp 10

2

ID

Itz Devils

13 tháng 10 2019

https://i.imgur.com/LLCr6oH.jpg

ID

Itz Devils

13 tháng 10 2019

https://i.imgur.com/nm7bkDH.jpg

Các câu hỏi dưới đây có thể giống với câu hỏi trên

T

tranquang

22 tháng 9 2019

cho tam giác ABC , M là điểm thuộc cạnh BC sao cho MB=2MC. Phân tích vecto AM theo vecto AB=u, AC =v

#Toán lớp 10

1

HT

Hoàng Tử Hà

22 tháng 9 2019

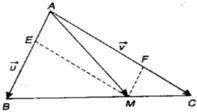
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\)

Có \(\overrightarrow{MB}=2\overrightarrow{MC}\Leftrightarrow\overrightarrow{MA}+\overrightarrow{AB}=2\overrightarrow{MA}+2\overrightarrow{AC}\)

\(\Leftrightarrow\overrightarrow{AM}=2\overrightarrow{AC}+\overrightarrow{BA}\)

PT

Pham Trong Bach

26 tháng 9 2018

Cho tam giác ABC. Điểm M nằm trên cạnh BC sao cho MB = 2MC. Hãy phân tích vectơ A M → theo hai vectơ u → = A B → ; v → = A C → ...

#Toán lớp 10

1

CM

Cao Minh Tâm

26 tháng 9 2018

Chọn B.

Ta có

mà

PT

Pham Trong Bach

27 tháng 6 2018

Trên đường thẳng chứa cạnh BC của tam giác ABC lấy điểm M sao cho M B → = 1 3 M C → . Khi đó vectơ A M → biểu diễn theo các vectơ u → = A B → ; v → = A C → là A. A M → = 3 2 u → ...

#Toán lớp 10

1

CM

Cao Minh Tâm

27 tháng 6 2018

Ta có M B → = 1 3 M C → ⇔ 3 M B → = M C → ⇔ 3 B M → = C M →

A M → = A B → + B M → ⇒ 3 A M → = 3 A B → + 3 B M → ( 1 ) A M → = A C → + C M → ( 2 )

Lấy (1) trừ (2) ta được :

2 A M → = 3 A B → + 3 B M → − A C → + C M → = 3 A B → − A C → + ( 3 B M → − C M → ) = 3 A B → − A C → + 0 → = 3 A B → − A C → ⇒ A M → = 3 2 A B → − 1 2 A C → = 3 2 u → − 1 2 v →

Đáp án A

LD

Luận Đào

12 tháng 12 2021

Cho tam giác ABC có AB=3 AC=5 góc BAC=60°. Gọi M là điểm thuộc đoạn BC sao cho BM=2MC . Tính độ dài đoạn AM

#Toán lớp 10

1

NV

Nguyễn Việt Lâm

Giáo viên

12 tháng 12 2021

Áp dụng địnhlý hàm cos:

\(BC=\sqrt{AB^2+AC^2-2AB.AC.cosBAC}=\sqrt{19}\)

\(\Rightarrow cosB=\dfrac{AB^2+BC^2-AC^2}{2AB.BC}=\dfrac{\sqrt{19}}{38}\)

\(BM=2MC\Rightarrow BM=\dfrac{2}{3}BC=\dfrac{2\sqrt{19}}{3}\)

\(\Rightarrow AM=\sqrt{AB^2+BM^2-2AB.BM.cosB}=\dfrac{\sqrt{139}}{3}\)

TT

Thư Trần

28 tháng 6 2023

Cho tam giác ABC có AB = 5, BC = 6 và AC = 9. Gọi M là trung điểm của BC, N là điểm thuộc cạnh AC sao cho AC = 3NC. Tính tích vô hướng...

#Toán lớp 10

0

TN

tơn nguyễn

11 tháng 1 2021

cho tam giác ABC . gọi M là điểm thuộc cạnh AB , N là điểm thuộc cạnh AC sao cho AM =\(\dfrac{1}{3}\) AB , AN =\(\dfrac{3}{4}\) AC . gọi O là giao điểm của CM và BN a) Biểu diễn vecto \(\overrightarrow{AO}\) theo 2 vecto \(\overrightarrow{AB}\) và \(\overrightarrow{AC}\)b) trên đường thẳng BC lấy E . Đặt \(\overrightarrow{BE}\)= x.\(\overrightarrow{BC}\) . tìm x để A,O ,E thẳng...

#Toán lớp 10

1

NT

Ngô Thành Chung

12 tháng 1 2021

undefined

undefined

Lười đánh máy nên luyện chữ :))

QN

Quỳnh Như Trần Thị

12 tháng 9 2021

Cho tam giác ABC. Điểm M nằm trên cạnh BC sao cho MB = 2MC. Hãy phân tích vectơ \(\overrightarrow{AM}\) qua 2 vecto \(\overrightarrow{AB,}\overrightarrow{AC}\)

#Toán lớp 10

2

AH

Akai Haruma

Giáo viên

13 tháng 9 2021

Lời giải:

Theo đề ta có: $\overrightarrow{BM}=2\overrightarrow{MC}=-2\overrightarrow{CM}$

$\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}(1)$

$=\overrightarrow{AB}-2\overrightarrow{CM}$

$\overrightarrow{AM}=\overrightarrow{AC}+\overrightarrow{CM}$

$\Rightarrow 2\overrightarrow{AM}=2\overrightarrow{AC}+2\overrightarrow{CM}(2)$

Lấy $(1)+(2)\Rightarrow 3\overrightarrow{AM}=\overrightarrow{AB}+2\overrightarrow{AC}$

$\Rightarrow \overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}$

AH

Akai Haruma

Giáo viên

13 tháng 9 2021

Hình vẽ:

NP

Ngô phương anh

18 tháng 7 2023

Cho tam giác ABC vuông tại A, điểm M thuộc AB sao cho góc CMB = 135° , biết MB=2, BC= 10 . Tính AM và AC

#Toán lớp 10

1

NL

Nguyễn Lê Phước Thịnh

22 tháng 7 2023

\(cosCMB=\dfrac{BM^2+MC^2-BC^2}{2\cdot BM\cdot MC}\)

=>\(2^2-10^2+MC^2=2\cdot2\cdot MC\cdot cos135\)

=>\(MC^2+2\sqrt{2}\cdot MC-96=0\)

=>\(MC=6\sqrt{2}\left(cm\right)\)

góc AMC=180-135=45 độ

=>ΔAMC vuông cân tại A

=>\(AM=MC\cdot sin45=6\sqrt{2}\cdot\dfrac{1}{\sqrt{2}}=6\left(cm\right)\)

=>AC=6(cm)

NH

Nguyễn Hương Linh

13 tháng 9 2021

Bài 12. Cho tam giác ABC. M là điểm thuộc cạnh BC sao cho 3BM = 7CM. Biểu diễn vecto AM qua vecto AB và AC .
.

#Toán lớp 10

4

NV

Nguyễn Việt Lâm

Giáo viên

13 tháng 9 2021

\(3BM=7CM=7\left(BC-BM\right)\Rightarrow10BM=7BC\)

\(\Rightarrow BM=\dfrac{7}{10}BC\Rightarrow\overrightarrow{BM}=\dfrac{7}{10}\overrightarrow{BC}\)

Ta có:

\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{AB}+\dfrac{7}{10}\overrightarrow{BC}=\overrightarrow{AB}+\dfrac{7}{10}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)=\overrightarrow{AB}-\dfrac{7}{10}\overrightarrow{AB}+\dfrac{7}{10}\overrightarrow{AC}\)

\(\Rightarrow\overrightarrow{AM}=\dfrac{3}{10}\overrightarrow{AB}+\dfrac{7}{10}\overrightarrow{AC}\)

AH

Akai Haruma

Giáo viên

13 tháng 9 2021

Lời giải:

Theo đề thì $\overrightarrow{3BM}=7\overrightarrow{MC}=-7\overrightarrow{CM}$

Lại có:

$\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}$

$\Rightarrow 3\overrightarrow{AM}=3\overrightarrow{AB}+3\overrightarrow{BM}=3\overrightarrow{AB}-7\overrightarrow{CM}(1)$

$\overrightarrow{AM}=\overrightarrow{AC}+\overrightarrow{CM}$

$\Rightarrow 7\overrightarrow{AM}=7\overrightarrow{AC}+7\overrightarrow{CM}(2)$

Từ $(1);(2)\Rightarrow 10\overrightarrow{AM}=3\overrightarrow{AB}+7\overrightarrow{AC}$

$\Rightarrow \overrightarrow{AM}=\frac{3}{10}\overrightarrow{AB}+\frac{7}{10}\overrightarrow{AC}$