Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

minh dang nghi cau a con cau b minh ra r ban co can k
b)me=1/3mn bf=1/3bcmn//bc
=>me//bf
=>e la trung diem cua af
=> AEF thang hang

Do M và N lần lượt là trung điểm của BC và AC nên MN là đường trung bình của tam giác AB.

Đáp án B

a.
\(\overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{BA}+\frac{1}{2}\overrightarrow{BC}+\frac{1}{2}\overrightarrow{CA}+\frac{1}{2}\overrightarrow{CB}\)
\(=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{BA}\right)+\frac{1}{2}\left(\overrightarrow{BC}+\overrightarrow{CB}\right)+\frac{1}{2}\left(\overrightarrow{AC}+\overrightarrow{CA}\right)=\overrightarrow{0}\)
b.
Ta có:
\(\overrightarrow{GM}+\overrightarrow{GN}+\overrightarrow{GP}=\overrightarrow{GA}+\overrightarrow{AM}+\overrightarrow{GB}+\overrightarrow{BN}+\overrightarrow{GC}+\overrightarrow{CP}\)
\(=\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)+\left(\overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP}\right)=\overrightarrow{0}+\overrightarrow{0}=\overrightarrow{0}\)
\(\Rightarrow G\) là trọng tâm tam giác MNP

a)
MN là đường trung bình của tam giác ABC nên \(\overrightarrow{MN}=\dfrac{1}{2}\overrightarrow{AC}\).
QP là đường trung bình của tam giác ABC nên \(\overrightarrow{QP}=\dfrac{1}{2}\overrightarrow{AC}\).
Vậy \(\overrightarrow{MN}=\overrightarrow{QP}\).
b) Giả sử:
\(\overrightarrow{MP}=\overrightarrow{MN}+\overrightarrow{MQ}\Leftrightarrow\overrightarrow{MP}-\overrightarrow{MN}-\overrightarrow{MQ}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{MP}+\overrightarrow{NM}+\overrightarrow{QM}=\overrightarrow{0}\)
\(\Leftrightarrow\left(\overrightarrow{QM}+\overrightarrow{MP}\right)+\overrightarrow{NM}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{QP}+\overrightarrow{NM}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{QP}-\overrightarrow{MN}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{QP}-\overrightarrow{QP}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{0}=\overrightarrow{0}\) ( Điều giả sử đúng).
Vậy \(\overrightarrow{MP}=\overrightarrow{MN}+\overrightarrow{MQ}.\)
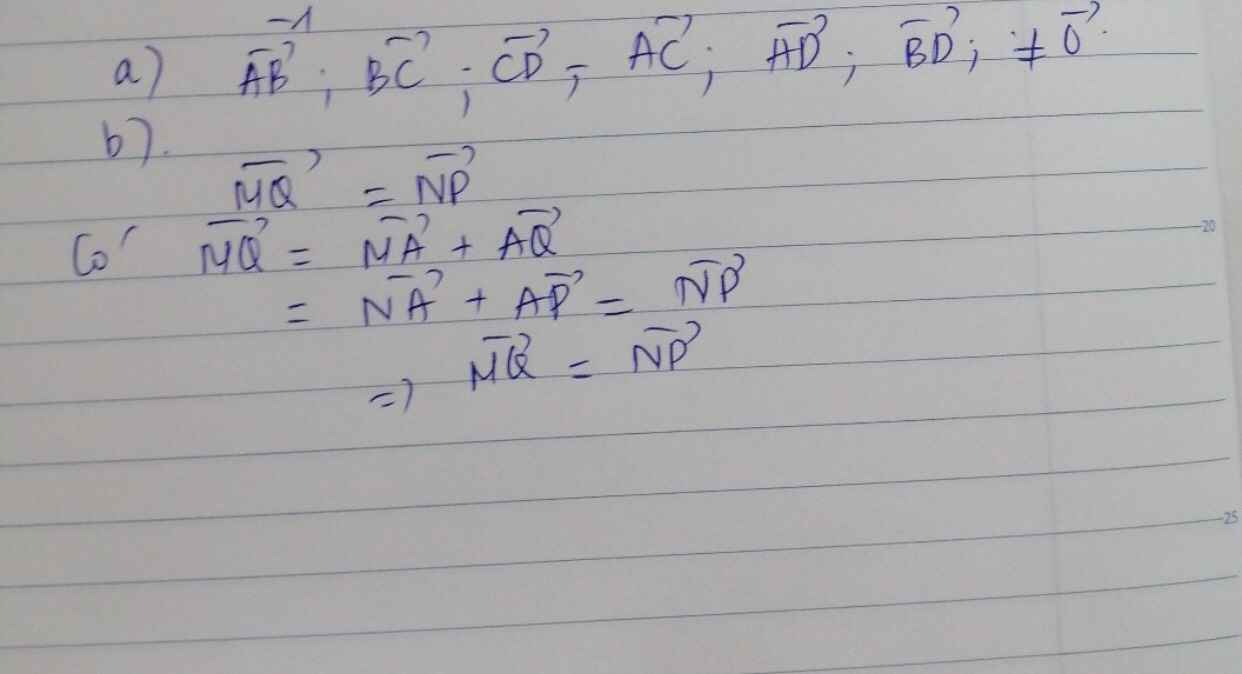
M là trung điểm AB \(\Rightarrow\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}\)
N là trung điểm AC \(\Rightarrow\overrightarrow{AN}=\dfrac{1}{2}\overrightarrow{AC}\)
P là trung điểm MN \(\Rightarrow\overrightarrow{PM}+\overrightarrow{PN}=\overrightarrow{0}\) \(\Rightarrow\overrightarrow{PA}+\overrightarrow{AM}+\overrightarrow{PA}+\overrightarrow{AN}=\overrightarrow{0}\)
\(\Rightarrow\overrightarrow{AM}+\overrightarrow{AN}=-2\overrightarrow{PA}=2\overrightarrow{AP}\)
\(\Rightarrow\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}=2\overrightarrow{AP}\Rightarrow\overrightarrow{AP}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\)
Q là trung điểm BC \(\Rightarrow\overrightarrow{QB}+\overrightarrow{QC}=\overrightarrow{0}\) \(\Rightarrow\overrightarrow{QA}+\overrightarrow{AB}+\overrightarrow{QA}+\overrightarrow{AC}=\overrightarrow{0}\)
\(\Rightarrow\overrightarrow{AB}+\overrightarrow{AC}=-2\overrightarrow{QA}=2\overrightarrow{AQ}\)
\(\Rightarrow\overrightarrow{AQ}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}=2\left(\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\right)=2\overrightarrow{AP}\)
\(\Rightarrow A;P;Q\) thẳng hàng