Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ AH⊥BC tại H
Xét ΔABD có
AH là đường cao ứng với cạnh BD(AH⊥BC, D∈BC)
nên \(S_{ABD}=\dfrac{AH\cdot BD}{2}\)
Xét ΔACD có
AH là đường cao ứng với cạnh CD(AH⊥BC, D∈BC)
nên \(S_{ACD}=\dfrac{AH\cdot CD}{2}\)
Ta có: \(\dfrac{S_{ABD}}{S_{ACD}}=\dfrac{AH\cdot BD}{2}:\dfrac{AH\cdot CD}{2}\)
\(\Leftrightarrow\dfrac{S_{ABD}}{S_{ACD}}=\dfrac{AH\cdot BD}{2}\cdot\dfrac{2}{AH\cdot CD}=\dfrac{BD}{CD}\)(1)
Xét ΔABC có
AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\)(2)
Từ (1) và (2) suy ra \(\dfrac{S_{ADB}}{S_{ADC}}=\dfrac{AB}{AC}\)
Vậy: Tỉ số diện tích của hai tam giác này bằng tỉ số giữa hai cạnh kề hai đoạn thẳng được tạo bởi tia phân giác kẻ xuống cạnh tương ứng

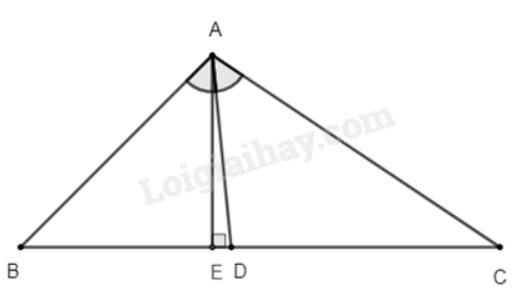
a) Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 10 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{10 - BD}} = \frac{6}{8} \Leftrightarrow 8BD = 6.\left( {10 - BD} \right) \Rightarrow 8BD = 60 - 6BD\)
\( \Leftrightarrow 8BD + 6BD = 60 \Leftrightarrow 14BD = 60 \Rightarrow BD = \frac{{60}}{{14}} = \frac{{30}}{7}\)
\( \Rightarrow DC = 10 - \frac{{30}}{7} = \frac{{40}}{7}\)
Vậy \(BD = \frac{{30}}{7}cm;DC = \frac{{40}}{7}cm\).
b) Kẻ \(AE \bot BC \Rightarrow AE\) là đường cao của tam giác \(ABC\).
Vì \(AE \bot BC \Rightarrow AE \bot BD \Rightarrow AE\)là đường cao của tam giác \(ADB\)
Diện tích tam giác \(ADB\) là:
\({S_{ADB}} = \frac{1}{2}BD.AE\)
Vì \(AE \bot BC \Rightarrow AE \bot DC \Rightarrow AE\)là đường cao của tam giác \(ADC\)
Diện tích tam giác \(ADC\) là:
\({S_{ADC}} = \frac{1}{2}DC.AE\)
Ta có: \(\frac{{{S_{ADB}}}}{{{S_{ADC}}}} = \frac{{\frac{1}{2}AE.BD}}{{\frac{1}{2}AE.CD}} = \frac{{BD}}{{DC}} = \frac{{\frac{{30}}{7}}}{{\frac{{40}}{7}}} = \frac{3}{4}\).
Vậy tỉ số diện tích giữa \(\Delta ADB\) và \(\Delta ADC\) là \(\frac{3}{4}\).

ta co: AB2+AC2=100 Ma BC2=100
\(\Rightarrow\Delta ABC\)vuong tai A
A, Trong \(\Delta ABC\)co AD la phan giac
\(\Rightarrow\frac{AB}{AC}=\frac{BD}{DC}\)(tinh chat duong phan giac)
\(\Rightarrow\frac{AB}{AB+AC}=\frac{BD}{BD+DC}\)\(\Rightarrow\frac{8}{8+6}=\frac{BD}{10}\Rightarrow BD=\frac{8.10}{14}=\frac{40}{7}cm\)
ta co: BD+DC=BC\(\Rightarrow DC=BC-BD=10-\frac{40}{7}=\frac{30}{7}cm\)
B, Ke duong cao AH
ta co: \(S_{\Delta ABD}=\frac{1}{2}AH.BD\)va \(S_{\Delta ACD}=\frac{1}{2}AH.DC\)
\(\Rightarrow\frac{S_{\Delta ABD}}{S_{\Delta ACD}}=\frac{\frac{1}{2}AH.BD}{\frac{1}{2}AH.DC}=\frac{BD}{DC}=\frac{40}{7}:\frac{30}{7}=\frac{4}{3}\)

a, Theo tính chất đường phân giác ta có : \(\frac{AD}{AB}=\frac{DC}{BC}\)=> \(\frac{AD}{4}=\frac{DC}{6}\)=> \(\frac{AD}{2}=\frac{DC}{3}=\frac{AD+DC}{2+3}=\frac{AC}{5}=\frac{5}{5}=1\)
=> \(\hept{\begin{cases}AD=2\\DC=3\end{cases}}\)
a) Áp dụng tính chất đường phân giác ta có:
\(\frac{AD}{CD}=\frac{AB}{BC}=\frac{4}{6}=\frac{2}{3}\)
\(\Leftrightarrow\frac{AD}{2}=\frac{AB}{3}=\frac{AD+AB}{2+3}=1\)
\(\Leftrightarrow AD=2;AB=3\)

a) Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{AB}{BD}=\dfrac{AC}{CD}\)(Tính chất đường phân giác của tam giác)
\(\Leftrightarrow\dfrac{6}{4.5}=\dfrac{8}{BD}\)
\(\Leftrightarrow BD=\dfrac{8\cdot4.5}{6}=\dfrac{36}{6}=6\left(cm\right)\)
Vậy:BD=6cm
b) Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{AB}{BD}=\dfrac{AC}{CD}\)(Tính chất đường phân giác của tam giác)
\(\Leftrightarrow\dfrac{8}{BD}=\dfrac{6}{CD}\)
mà BD+CD=BC(D nằm giữa B và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{8}{BD}=\dfrac{6}{CD}=\dfrac{8+6}{BD+CD}=\dfrac{14}{BD}=\dfrac{14}{7}=2\)
Do đó:
\(\dfrac{6}{CD}=2\)
hay CD=3(cm)
Vậy: CD=3cm

Lời giải: Đề bài có vẻ thừa dữ kiện.
Theo tính chất tia phân giác:
a)
$\frac{S_{ADB}}{S_{ADC}}=\frac{BD}{DC}=\frac{6}{4,5}=\frac{4}{3}$
b)
$\frac{S_{ADB}}{S_{ADC}}=\frac{BD}{DC}=\frac{BC-DC}{DC}=\frac{7-3}{3}=\frac{4}{3}$