Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) xét tam giác ADB và AEC có:
góc A chung
góc ADB= góc AEC (=90 độ)
=> ADB đồng dạng vs AEC (g.g)
b) xét tam giác EHB và tam giác DHC có:
EHB= DHC (2 góc đối đỉnh)
HEB- HDC (=90độ)
=> EHB =DHC (g.g)
=> HE/HB = HD/HC
=> HE.HC=HD.HB

a: Xét ΔABH vuông tại H và ΔDBH vuông tại H có
BH chung
HA=HD
Do đó: ΔABH=ΔDBH
b: Xét ΔHAE vuông tại H và ΔHDB vuông tại H có
HA=HD
góc HAE=góc HDB
Do đó: ΔHAE=ΔHDB
=>HE=HB
Xét tứ giác ABDE có
H là trung điểm chung của AD và BE
nên ABDE là hình bình hành
=>AB//DE

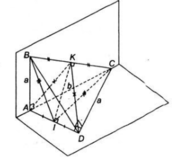


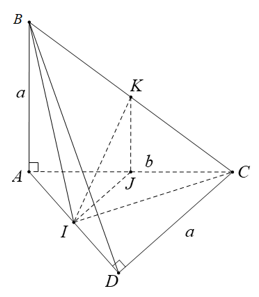
Chứng minh tương tự, ta có tam giác AKD là tam giác cân tại K có KI là đường trung tuyến nên đồng thời là đường cao.
⇒ IK ⊥ AD (2)
Từ (1) và (2) suy ra; IK là đường vuông góc chung của hai đường thẳng AD và BC.






a: Xét ΔBAD có
BH vừa là đường cao, vừa là trungtuyến
nên ΔBAD cân tại B
=>BH là phân giác của góc ABD
b: Xét ΔBAC và ΔBDC có
BA=BD
góc ABC=góc DBC
BC chung
Do đó: ΔBAC=ΔBDC
=>góc BDC=90 độ
=>BD vuông góc với DC
c: Xét tứ giác ACDE có
H là trung điểm chung của AD và CE
nên ACDE là hình bình hành
=>DE//AC
=>DE vuông góc với AB