Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔABD và ΔEBD có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔABD=ΔEBD(c-g-c)
b) Ta có: ΔABD=ΔEBD(cmt)
nên \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BED}=90^0\)

A B C D E F
a/ Xét \(\Delta ABD\)và \(\Delta EBD\)
BA=BE (gt); BD chung
\(\widehat{ABD}=\widehat{EBD}\)(gt)
\(\Rightarrow\Delta ABD=\Delta EBD\left(c.g.c\right)\)
b/
\(\Delta ABD=\Delta EBD\left(cmt\right)\Rightarrow\widehat{BAD}=\widehat{BED}=90^o\Rightarrow DE\perp BC\)
c/
Ta có
BE=BA (gt); AF=CE (gt)
=> BE+CE=BA+AF => BC=BF => tg BCF cân tại B
Mà BD là phân giác \(\widehat{ABC}\)
\(\Rightarrow BD\perp CF\) (trong tg cân đường phân giác của góc ở đỉnh đồng thời là đường cao)
Mà \(CA\perp BF\)
=> D là trực tâm của \(\Delta BCF\Rightarrow FD\perp BC\) mà \(DE\perp BC\) => FD trùng DE (từ 1 điểm ngoài đường thẳng chỉ dựng được duy nhất 1 đường thẳng vuông góc với đường thẳng đã cho) => E, D, F thẳng hàng
hình vào tcn cho mình thay G là điểm D vì mình nhầm trọng tâm của tam giác
a) Xét tam giác ABD và tam giác EBD có:
AB=BE (gt)
^ABD=^EBD (^ABD là tia phân giác)
BD chung
=> tam giác ABD = tam giác EBD ( c.g.c )
b) Vì ABC là tam giác vuông tại A
=> tam giác ABD là tam giác vuông tại A
Mà: tam giác ABD = tam giác EBD ( c.g.c )
=> ^BED=^BAD= 90o
=> DE_|_BC (đpcm)
c) Nối F và C lại với nhau
Vì: FA=FB ( gt)
Mà CA_|_FB ( tam giác ABC _|_ tại A)
=> CA là đg trung trực của tam giác ABC
=> CA là đg trung tuyến của tam giác ABC
Mà tia phân giác ABC cắt AC tại D
=> D là trọng tâm của tam giác ABC
=> D,E,F thằng hàng (đpcm)

BCEDAF
*Hình quên đánh dấu ABD = DBE nhé
*Cần viết gt và kl thì bảo mình nhá <3
Giải
a) Xét ∆ABD và ∆EBD có :
AB = BE (gt) |
FBD = DBE (AD là tia phân giác ABE) }
BD là cạnh chung |
=> ∆ABD = ∆EBD (c.g.c)

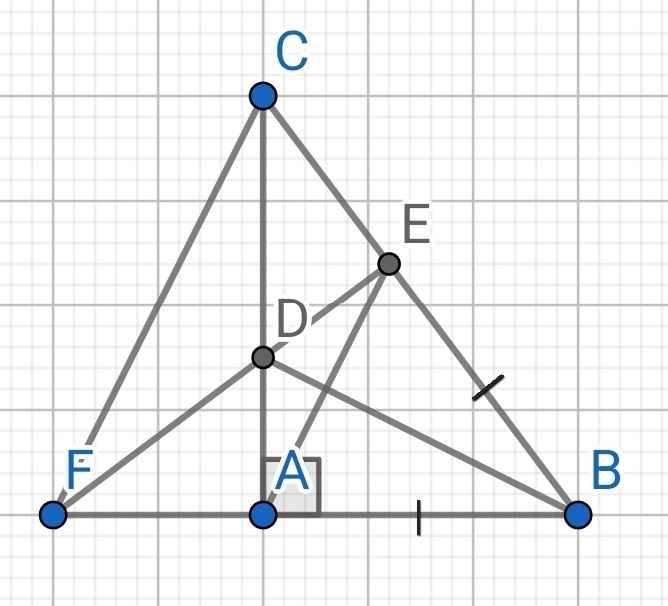 a) Xét ∆ABD và ∆EBD có:
a) Xét ∆ABD và ∆EBD có:
AB = BE (gt)
∠ABD = ∠EBD (BD là tia phân giác của ABC)
BD là cạnh chung
⇒ ∆ABD = ∆EBD (c-g-c)
b) Do ∆ABD = ∆EBD (cmt)
⇒ AD = ED (hai cạnh tương ứng)
Lại do ∆ABD = ∆EBD (cmt)
⇒ ∠BAD = ∠BED = 90⁰ (hai góc tương ứng)
⇒ ∠DAF = ∠DEC = 90⁰
Xét hai tam giác vuông: ∆DAF và ∆DEC có:
AD = ED (cmt)
∠ADF = ∠EDC (đối đỉnh)
⇒ ∆DAF = ∆DEC (cạnh góc vuông - góc nhọn kề)
⇒ AF = EC (hai cạnh tương ứng)
c) ∆BAE có:
AB = BE (gt)
⇒ ∆BAE cân tại B
⇒ ∠BEA = ∠BAE = (180⁰ - ∠ABC) : 2 (1)
Do AF = EC (cmt)
AB = BE (gt)
⇒ AF + AB = EC + BE
⇒ BF = BC
⇒ ∆BFC cân tại B
⇒ ∠BCF = ∠BFC = (180⁰ - ∠ABC) : 2 (2)
Từ (1) và (2) suy ra:
∠BEA = ∠BCF
Mà ∠BEA và ∠BCF là hai góc đồng vị
⇒ AE // CF

Câu a,b: dễ bạn tự làm nhé
c) Ta có tam giác BAE = tam giác BDE ( cm b)
=> góc CAB = góc BDF (2 góc t/ư)
Mà góc CAB = 90*( vì tam giác ABC vuông tại A)
=> góc BDF =90*
\(\Rightarrow\hept{\begin{cases}ED\perp BC\\FD\perp BC\end{cases}}\)(ĐN)
=> D, E, F thẳng hàng ( cùng \(\perp\)BC)

a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
=>\(\widehat{BED}=\widehat{BAD}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BED}=90^0\)
b: ΔBAD=ΔBED
=>DA=DE
Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó: ΔDAF=ΔDEC
=>DF=DC
Xét ΔABDΔABD và ΔEBDΔEBD, ta có:
AB=BE ( gt)
ABDˆ=EBDˆABD^=EBD^ ( Vì BD là tia phân giác của góc B)
BD chung
⇒ΔABD=ΔEBD⇒ΔABD=ΔEBD (c-g-c)