Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

giangtruong2922/08/2020
Đáp án:
Giải thích các bước giải:
a)Do tam giác ABC vuông tại B mà AB=8cm;BC=6cmAB=8cm;BC=6cm
=> theo Pitago ta có: AC=AB2+BC2−−−−−−−−−−√=10AC=AB2+BC2=10
Gọi H là trung điểm của BD => B đối xứng D qua H
Xét tam giác CHBCHB và tam giác CHDCHD có:
HB=HDHB=HD (gt)
góc CHBCHB = góc CHDCHD
CHCH: chung
=> tam giác CHB = tam giác CHD (c.g.c ) => CB=CD=6CB=CD=6
Hoàn toàn tương tự ta có :
tam giác AHBAHB = tam giác AHDAHD (c.g.c) => AB=AD=8AB=AD=8
Xét tam giác ADC có AD=8;CD=6;AC=10AD=8;CD=6;AC=10
=> Theo Định lý Pitago đảo ta có:
=> AD2+CD2=AC2AD2+CD2=AC2
=> Tam giác ADC vuông tại D
=> Xét tứ giác ABCD có:
góc ABCABC = góc ADCADC = 90o90o
=> góc ABCABC +góc ADCADC =180o180o
=> tứ giác ABCD là tứ giác nội tiếp
=> A,B,C,D cùg thuộc đường tròn (ABC) (Đpcm)
b)Do ABC là tam giác vuông; A, B, C cùng thuộc đường tròn => AC là đường kính
Lấy O là tâm đường tròn => O là trung điểm AC
Bán kính đường tròn: OA=OB=AC2=5(cm)
Hình như mấy đứa nhóc trẩu trẩu thích đi buff SP với cả fl thì phải :)

a: D đối xứng B qua AC
=>AC là trung trực của BD
=>AB=AD và CB=CD
Xét ΔABC và ΔADC có
AB=AD
BC=DC
AC chung
Do đó; ΔABC=ΔADC
=>góc ABC=góc ADC=90 độ
Xét tứ giác ABCD có
góc ABC+góc ADC=90 độ+90 độ=180 độ
=>ABCD nội tiếp đường tròn đường kính AC
b: ΔABC vuông tại B
=>AC^2=AB^2+BC^2
=>AC^2=8^2+6^2=10^2
=>AC=8cm
=>R=8/2=4cm


KH cắt BD tại M
Ta có HI//AC//ND ( cùng \(\perp AB\)) \(\Rightarrow\widehat{C}=\widehat{H_2}\) (đồng vị) và \(\widehat{H_1}=\widehat{H_3}\) (đối đỉnh)
K là trung điểm AC và \(\Delta AHC\) vuông tại H \(\Rightarrow\)KH = KC \(\Rightarrow\Delta KHC\) cân tại K
\(\Rightarrow\widehat{C}=\widehat{H_3}=\widehat{H_1}=\widehat{H_2}\Rightarrow\Delta BHI=\Delta BHM\left(ch-gn\right)\)(có \(\widehat{H_1}=\widehat{H_2}\)HB chung)
\(\Rightarrow\widehat{BIH}=\widehat{BMH}=90^0\Rightarrow HM\perp BD\)
\(\Rightarrow\)BH = BM.MD (hệ thức lượng trong \(\Delta BHD\) vuông tại H)
Mà \(\Delta BMK~\Delta BTD\left(g.g\right)\) ( có \(\widehat{BMK}=\widehat{BTD}=90^0\) và góc B chung)
\(\Rightarrow\)BM.BD = BT.BK = BH
Vì BH =BI.BA (hệ thức lượng trong \(\Delta BHA\) vuông tại H)
\(\Rightarrow\)BT.BK=BI.BA \(\Rightarrow\Delta TBI~\Delta ABK\left(c-g-c\right)\)(có góc B chung và \(\frac{BT}{BI}=\frac{BK}{BA}\))
\(\Rightarrow\widehat{BTI}=\widehat{BAK}=90^0\Rightarrow TI\perp BK\)tại T
\(\Rightarrow\Delta BDT\) nội tiếp (J) có cạnh BD là đường kính \(\Rightarrow\Delta BDT\)vuông tại T
\(\Rightarrow TD\perp BK\) tại T \(\Rightarrow\)Từ T có TI và TD cùng \(\perp\) BK suy ra 3 điểm D, T, I thẳng hàng.

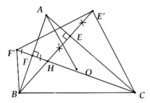
a, ∆CHE' cân tại C => C E ' H ^ = C H E ' ^
DBHF' cân tại B => B F ' H ^ = B H F ' ^
Mà => C H E ' ^ = B H F ' ^ (đối đỉnh)
=> C E ' H ^ = B F ' H ^
=> Tứ giác BCE'F' nội tiếp đường tròn tâm (O)
b, Có B F C ' ^ = B E ' C ^ = C H E ' ^ = C A B ^
Vậy A, F', E' cùng chắn BC dưới góc bằng nhau
=> 5 điểm B, F', A, E', C cùng thuộc một đường tròn tâm (O)
c, AF' = AE' (=AH) => AO là trung trực của EF => AO ^ E'F'. DHE'F' có EF là đường trung bình => EF//E'F'
=> AO ^ FE
d, A F H ^ = A E H ^ = 90 0 => AFHE nội tiếp đường tròn đường kính AH. Trong (O): Kẻ đường kính AD, lấy I trung điểm BC
=> OI = 1 2 AH, BC cố định => OI không đổi
=> Độ dài AH không đổi
=> Bán kính đường tròn ngoại tiếp ∆AEF không đổi
Đó là đường tròn có tâm là trung điểm của AC