Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, tam giác ABC vuông tại B có góc A = 30 độ => AC = 2 BC = 2. 3 = 6 cm
theo định lí Pytago ta có AB = \(\sqrt{ÃC^2-BC^2}=\sqrt{6^2-3^2}\) = \(3\sqrt{3}\) cm
góc C = 90 - 30 = 60 độ
b, tam giác ABH vuông tại H có góc A = 30 độ => AB = 2 BH => BH = \(\frac{3\sqrt{3}}{2}\)cm
theo định lí Pytago ta có AH = \(\sqrt{AB^2-BH^2}=\sqrt{\left(3\sqrt{3}\right)^2-\left(\frac{3\sqrt{3}}{2}\right)^2}=4,5cm\)
diện tích tam giác ABH =\(\frac{1}{2}.BH.AH=\frac{1}{2}.\frac{3\sqrt{3}}{2}.4,5=\frac{27\sqrt{3}}{8}\)cm vuông

AB=21/(3+4)x3=9 cm
AC=21-9=12cm
Tự kẻ hình bạn nhé =)))
Áp dụng định lí Pitago vào tam giác ABC , có
AB^2+AC^2=BC^2
=>thay số vào, tính được BC=15cm
Áp dụng hệ thức giữa cạnh và đường cao trong tg vuông, có:
AB^2=BHxBC
=>BH=81/15=5.4cm
=>CH=15-5.4=9.6cm
AH^2=BHxCH=5.4x9.6=51.84cm

mình chỉ biết bài 3 thôi. hai bài kia cx làm được nhưng ngại trình bày
A B C 4 9
Ta có : BC = BH +HC = 4 + 9 = 13 (cm)
Theo hệ thức lượng trong tam giác vuông ta có:
- AC2 = BC * HC
AC2 = 13 * 9 = 117
AC = \(3\sqrt{13}\)(cm)
- AB2 =BH * BC
AB2 = 13 * 4 = 52
AB = \(2\sqrt{13}\)(CM)

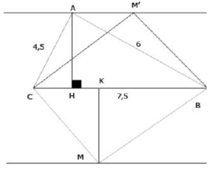
a) Ta có: A B 2 + A C 2 = 6 2 + 4 , 5 2 = 7 , 5 2 = B C 2
nên tam giác ABC vuông tại A. (đpcm)
![]()
= > ∠ B = 37 ° = > ∠ C = 90 ° - ∠ B = 90 ° - 37 ° = 53 °
Mặt khác trong tam giác ABC vuông tại A, ta có:
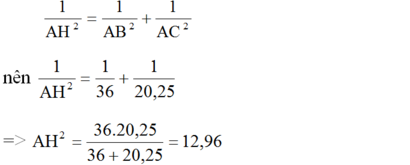
=> AH = 3,6 cm
b) Gọi khoảng cách từ M đến BC là MK. Ta có:
![]()
Ta thấy SMBC = SABC khi MK = AH = 3,6 cm
Do đó để SMBC = SABC thì M phải nằm trên đường thẳng song song và cách BC một khoảng là 3,6 cm (có hai đường thẳng như trên hình).

a, bạn dễ dàng chứng minh được tam giác ABC vuông tại A theo định lí Py-ta-go đảo
-áp dụng tỉ số lượng giác sinB = \(\frac{4,5}{7,5}\)=> góc B= 37o => góc C = 53o
-áp dụng HTL cho tam giác vuông ABC có đường cao AH: AH.BC = AB.AC => AH = 3,6 (cm)

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
c: \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot4.5}{2}=3\cdot4.5=13.5\left(cm^2\right)\)
a: góc A=90-60=30 độ
Xét ΔABC vuông tại A có sin C=AB/AC
=>6/AC=sin60
=>AC=4*căn 3(cm)
=>BC=2*căn 3(cm)
b; S ABC=1/2*2căn 3*6=6căn 3(cm2)