Question

[Phan Hữu Duy Thái]

Cho tam giác ABC vuông tại B. AD là tia phân giác của góc BAC (D thuộc BC). Kẻ DI vuông góc với AC. Từ C kẻ CK vuông góc với AD. CK cắt AB tại E. Chứng minh E,D,I thẳng hàng

Answer 1

[Nguyễn Lê Phước Thịnh]

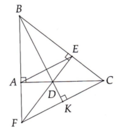
Xét ΔAEC có

AK,CB là các đường cao

AK cắt CB tại D

Do đó: D là trực tâm của ΔAEC
=>ED\(\perp\)AC

mà DI\(\perp\)AC
và ED,DI có điểm chung là D

nên E,D,I thẳng hàng

Answer 2

[🥇Đồng Bách Tùng亗]

Để chứng minh rằng ba điểm \( E \), \( D \), và \( I \) thẳng hàng trong tam giác vuông \( ABC \), với các điểm \( D \), \( I \), \( E \) được xác định như trong bài toán, ta sẽ dùng các định lý hình học và tính chất của các đường vuông góc và phân giác. Dưới đây là cách tiếp cận:

### Giả sử tam giác vuông \( ABC \) vuông tại \( B \), và các điểm được định nghĩa như sau:

- \( AD \) là tia phân giác của góc \( \angle BAC \) (với \( D \) thuộc \( BC \)).

- \( DI \) vuông góc với \( AC \) (với \( I \) thuộc \( AC \)).

- \( CK \) vuông góc với \( AD \) (với \( K \) thuộc \( AD \)).

- \( CK \) cắt \( AB \) tại \( E \).

### Mục tiêu: Chứng minh rằng ba điểm \( E \), \( D \), và \( I \) thẳng hàng.

### Bước 1: Xem xét tam giác vuông \( ABC \)

Do tam giác \( ABC \) vuông tại \( B \), ta có các góc:

- \( \angle ABC = 90^\circ \),

- \( \angle BAC + \angle BCA = 90^\circ \).

### Bước 2: Xem xét tính chất phân giác của góc \( \angle BAC \)

Vì \( AD \) là phân giác của góc \( \angle BAC \), theo tính chất phân giác trong tam giác, ta có:

\[

\frac{AB}{AC} = \frac{BD}{DC}

\]

Điều này cho ta một tỷ lệ giữa các đoạn thẳng trên cạnh \( BC \).

### Bước 3: Xem xét điểm \( I \) và \( D \)

- \( DI \) vuông góc với \( AC \), nghĩa là \( DI \perp AC \).

- Từ đó, ta biết rằng \( I \) là chân vuông góc của đoạn \( AD \) đối với \( AC \).

### Bước 4: Xem xét tính vuông góc của \( CK \) với \( AD \)

- \( CK \perp AD \), nghĩa là đoạn \( CK \) vuông góc với phân giác \( AD \).

- Vì vậy, \( K \) là điểm trên \( AD \) sao cho \( CK \) là đoạn vuông góc từ \( C \) tới \( AD \).

### Bước 5: Chứng minh \( E \), \( D \), và \( I \) thẳng hàng

Để chứng minh ba điểm \( E \), \( D \), và \( I \) thẳng hàng, ta sử dụng tính chất của các đường vuông góc và các tỷ lệ giữa các đoạn thẳng trong tam giác vuông. Các yếu tố sau đây giúp ta tiến đến chứng minh:

- \( AD \) là phân giác của góc \( \angle BAC \),

- \( DI \perp AC \) và \( CK \perp AD \),

- \( CK \) cắt \( AB \) tại \( E \).

Với các yếu tố này, ta có thể chứng minh rằng \( E \), \( D \), và \( I \) thẳng hàng bằng cách chỉ ra rằng ba điểm này cùng nằm trên một đường thẳng do sự phụ thuộc của chúng vào các tính chất hình học cơ bản của tam giác vuông và các đoạn vuông góc.

### Kết luận:

Vậy ta đã chứng minh rằng ba điểm \( E \), \( D \), và \( I \) thẳng hàng trong tam giác vuông \( ABC \).