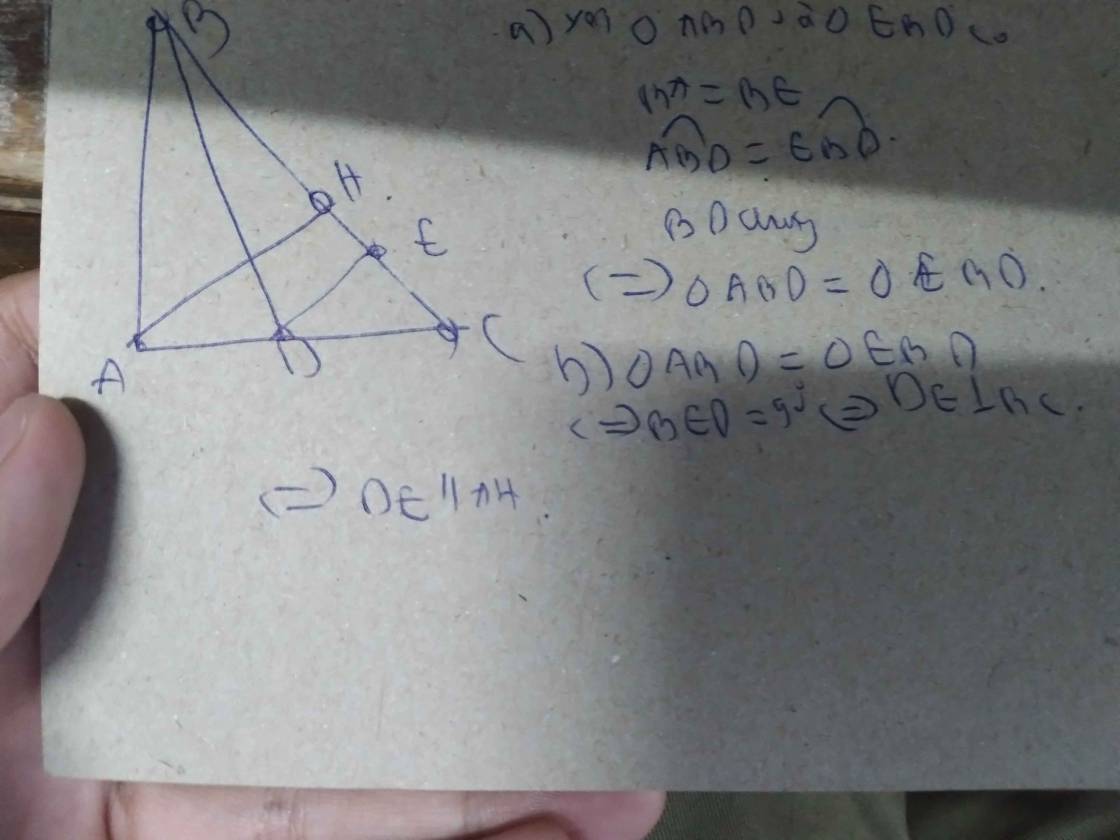Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
=>DA=DE và góc BED=góc BAD=90 độ
b; AH vuông góc BC
DE vuông góc BC
=>AH//DE

a) Xét tam giác BDA và tam giác BDE có:
cạnh BD chung(gt)
góc ABD=gócEBD(BD là tia phân giác góc B)
BA=BE(gt)
=>tam giác ABD=tam giác EBD(c.g.c)=>Đpcm
b) Theo a có tam giác ABD=tam giác EBD=>góc A= góc BED(2 góc tương ứng) =>góc A= góc BED(2 góc tương ứng)
Mà góc A=90 độ=>góc BED=90 độ=>Đpcm
c) Vì tam giác ABC vuông tại A(gt) =>góc B+góc C=90 độ (1)
Vì AH vuông góc với BC(gt) =>góc AHB =90 độ=>tam giác ABH vuông tại H=>góc B+góc BAH=90độ (2)
Từ (1) và (2) =>góc ACH= góc BAH=>Đpcm
Vì góc DEB=90 độ=>DE vuông góc với BC (*)
Mà AH vuông góc với BC (**)
Từ (*) và(**)=>DE // AH(quan hệ vuông góc-song song)=>Đpcm
d) Gọi H là giao của BD và AE
Xét tam giác BAH và tam giác BEH có
cạnh BH chung(gt)
góc ABH- góc EBH(gt)
BA=BE(gt)
=>tam giác ABH=tam giác EBH(c.g.c)
=>HA=HE(2 cạnh tương ứng) (4)
góc BHA=góc BHE
Mà góc BHE+góc BHE=180 độ(2 góc kề bù) => góc BHE=góc BHA=90 độ (3)
+ Từ (3) và(4)=> BD là đường trung trực của AE=>Đpcm


a)
ΔABDΔABD và ΔEBDΔEBD có:
BA = BE (gt)
ˆB1=ˆB2B1^=B2^ (BD là tia phân giác góc B)
BD là cạnh chung
⇒ΔABD=ΔEBD⇒ΔABD=ΔEBD (c.g.c)
⇒⇒ ˆBAD=ˆBEDBAD^=BED^ (hai góc tương ứng)
mà ˆBADBAD^ =900=900
⇒⇒ˆBEDBED^ =900=900
⇒⇒ DE ⊥

a) Xét tgiac ABD và EBD có:
+ AB = BE
+ BD chung
+ góc ABD = EBD
=> Tgiac ABD = EBD (c-g-c)
=> đpcm
b) Tgiac ABD = EBD (cmt) => AD = DE (hai cạnh t/ứng)
Xét tgiac ADE có AD = DE => Tgiac ADE cân tại D
=> đpcm
c) AH \(\perp\)BC, DE\(\perp\)BC => AH\(//\)DE
=> góc HAE = AED (2 góc SLT do AH\(//\)DE)
Mà tgiac ADE cân tại D (cmt) => góc AED = DAE
=> góc HAE = DAE
=> AE là tia pgiac góc HAC (đpcm)
d) Xét tgiac ADK và EDC có:
+ góc DAK = DEC = 90o
+ góc ADK = EDC (2 góc đối đỉnh)
+ AD = DE (do tgiac ABD = EBD)
=> Tgiac ADK = EDC (g-c-g)
=> AK = EC và KD = DC (2 cạnh t/ứng)
=> Tgiac KDC cân tại K => Góc DCK = (180o- góc KDC) /2
Tgiac AED cân tại D => góc EAD = (180o- góc ADE) /2
Mà góc ADE = KDC (2 góc đối đỉnh) => góc DCK = EAD
Mà 2 góc này SLT => AE \(//\)KC
=> đpcm