Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔCBA vuông tại B có
\(\tan\widehat{ACB}=\frac{AB}{BC}=\frac{6}{8}=\frac{3}{4}\)
\(\Rightarrow\widehat{ACB}\simeq36^052'\)
Vậy: \(\widehat{ACB}\simeq36^052'\)
b)
Áp dụng định lí Pytago vào ΔCBA vuông tại B, ta được:
\(AC^2=BA^2+BC^2\)
\(\Leftrightarrow AC^2=6^2+8^2=100\)
hay \(AC=\sqrt{100}=10\)
Xét ΔCBA có AD là tia phân giác của \(\widehat{BAC}\)(gt)
nên \(\frac{AB}{BD}=\frac{AC}{CD}\)(Tính chất đường phân giác của tam giác)
hay \(\frac{6}{BD}=\frac{10}{CD}\)
Ta có: BD+CD=BC(D nằm giữa B và C)
hay BD+CD=8
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\frac{6}{BD}=\frac{10}{CD}=\frac{6+10}{BD+CD}=\frac{16}{8}=2\)
\(\Leftrightarrow BD=\frac{6}{2}=3\)
Xét ΔABD vuông tại B có
\(\tan\widehat{ADB}=\frac{AB}{BD}=\frac{6}{3}=2\)

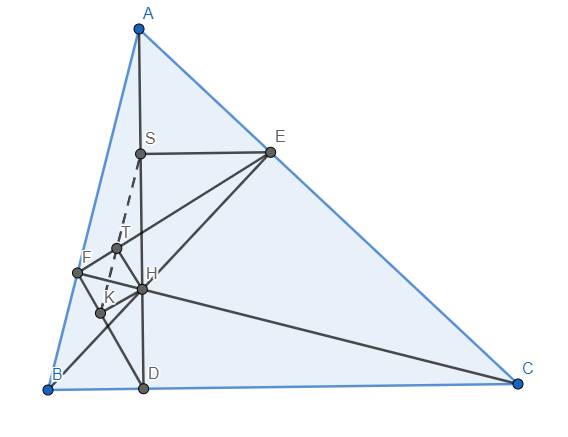
Tứ giác ESTH có \(\widehat{ETH}=\widehat{ESH}=90^o\) nên ESTH nội tiếp.
\(\Rightarrow\widehat{TSH}=\widehat{TEH}=\widehat{FEH}\)
Mà tứ giác AEHF nội tiếp \(\left(\widehat{AFH}=\widehat{AEH}=90^o\right)\) nên \(\widehat{FEH}=\widehat{FAH}\).
Từ đó suy ra \(\widehat{TSH}=\widehat{FAH}\) \(\Rightarrow\) TS//AB.
Mặt khác, tứ giác FTHK nội tiếp \(\left(\widehat{FTH}=\widehat{FKH}=90^o\right)\) nên \(\widehat{FTK}=\widehat{FHK}\) \(=90^o-\widehat{DFH}\) \(=90^o-\widehat{HBD}\) \(=\widehat{BHD}\) \(=\widehat{AHE}\) \(=\widehat{AFE}\) \(=\widehat{AFT}\) nên TK//AB.
Từ đó suy ra K, T, S thẳng hàng (tiên đề Euclid)
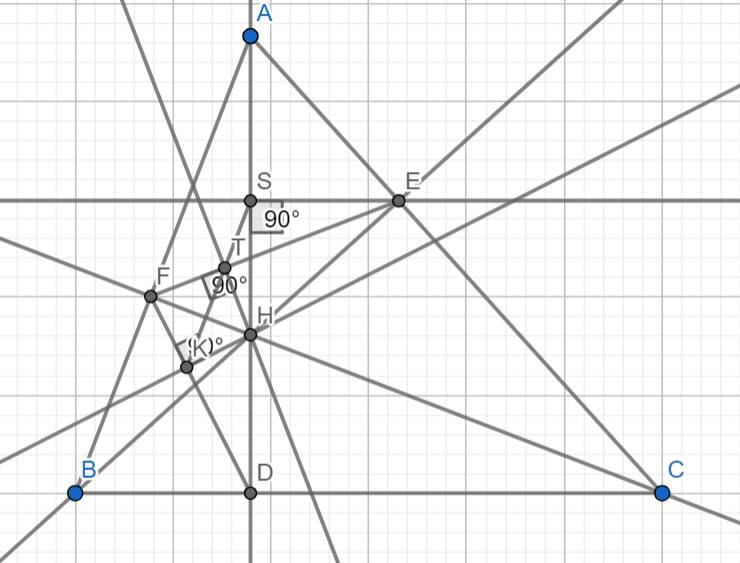
Dễ dàng chứng minh tứ giác HKFT nội tiếp: => \(\widehat{HTK}=\widehat{HFK}\)
Dễ dàng chứng minh tứ giác AFDC nội tiếp: => \(\overline{\widehat{HFK}=\widehat{HAE}}\)
Mà \(\widehat{HAE}=\widehat{HES}\) và \(\widehat{HES}+\widehat{HTS}=180\) (Dễ dàng c/m tứ giác HTSE nội tiếp)
Nên \(\widehat{HTK}+\widehat{HTS}=180\)=> 3 điểm K,T,S thẳng hàng
(Nếu chưa học tứ giác nội tiếp thì kéo dài FK và TH cắt tại điểm nào đó rồi chứng minh tam giác đồng dạng và suy ra góc như trên, tứ giác AFDC cũng vậy )

Kẻ DM, DN vuông góc với AB, AC.
Ta có: DNAB=CDBD⇒1AB=CDDN.BC;MDAC=BDBC⇒1AC=BDMD.BC⇒1AB+1AC=CD+BDDN.BC=1DNDNAB=CDBD⇒1AB=CDDN.BC;MDAC=BDBC⇒1AC=BDMD.BC⇒1AB+1AC=CD+BDDN.BC=1DN
Do AMDN là hình vuông nên: AD=√2DMAD=2DM =>ĐPCM
Câu b thì cm tương tự, mình để bạn tự giải !

kẻ đường cao AH ta có \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)
AD và AE là hai tia phân giác cả hai góc kề bù => AD _|_ AE
AH là đường cao của tam giác vuông ADE ta có
\(\frac{1}{AH^2}=\frac{1}{AD^2}+\frac{1}{AE^2}\)
vậy \(\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{AD^2}+\frac{1}{AE^2}\)
Ta có: \(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\)
Vì CD là phân giác trong góc C
\(\Rightarrow\dfrac{AD}{BD}=\dfrac{AC}{BC}\Rightarrow\dfrac{AD}{BD}=\dfrac{8}{10}=\dfrac{4}{5}\Rightarrow BD=\dfrac{5}{4}AD\)
Ta có: \(AD+BD=AB\Rightarrow AD+\dfrac{5}{4}AD=6\Rightarrow\dfrac{9}{4}AD=6\Rightarrow AD=\dfrac{8}{3}\)
Vì CD,CE lần lượt là phân giác trong và ngoài góc C
\(\Rightarrow CD\bot CE\Rightarrow\Delta DCE\) vuông tại C có \(AC\bot DE\)
\(\Rightarrow AD.AE=AC^2\Rightarrow AE=\dfrac{AC^2}{AD}=\dfrac{8^2}{\dfrac{8}{3}}=24\)