Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAHD có
AN là đường cao
AN là đường trung tuyến
Do đó:ΔAHD cân tại A
mà AB là đường trung tuyến
nên AB là tia phân giác của góc HAD(1)
Xét ΔAHE có
AM là đường cao
AM là đường trung tuyến
Do đó: ΔAHE cân tại A
mà AC là đường cao
nên AC là tia phân giác của góc HAE(2)
Từ (1) và (2) suy ra \(\widehat{DAE}=2\cdot\left(\widehat{BAH}+\widehat{CAH}\right)=2\cdot90^0=180^0\)
hay D,A,E thẳng hàng
b: Xét ΔHED có
M là trung điểm của HE
N là trung điểm của HD
Do đó: MN là đường trung bình
=>MN//ED
d: Xét ΔDHE có
HA là đường trung tuyến
HA=DE/2
Do đó:ΔDHE vuông tại H

a.
Xét tam giác AHM và tam giác DCM có:
AM = DM (gt)
AMH = DMC (2 góc đối đỉnh)
MH = MC (M là trung điểm của HC)
=> Tam giác AHM = Tam giác DCM (c.g.c)
b.
AHM = DCM (tam giác AHM = tam giác DCM)
mà AHM = 90độ
=> DCM = 90độ
Tam giác ABC vuông tại A có:
ABC + ACB = 90độ
60độ + ACB = 90độ
ACB = 90 - 60
ACB = 30độ
ACD = ACB + DCM = 30 + 90 = 120độ
a) C/M tam giác AHM= tam giác DCM
Xét tam giác AHM và tam giác DCM, ta có:
MA=MD (gt)
góc AMH= góc DMC (đđ)
MH=MC (gt)
Vậy tam giác AHM= tam giác DCM (c-g-c)
b) Tính góc ACD
Ta có tam giác ABC vuông tại A có góc B=600 nên góc ACB=300
Lại có góc MCD= góc AHM = 900 (hai tam giác bằng nhau)
Vậy góc ACD= 300 + 900 = 1200
c) C/M AK=CD
Trong tam giác AHK, ta có AN đường cao đồng thời là trung tuyến ( AN vuông góc HK và NH=NK)
Nên tam giác AHK cân tại A
Suy ra AK=AH
Mà AH=CD (hai tam giác bằng nhau)
Vậy AK=CD
d) C/M K, H, D thẳng hàng
Ta có tam giác AHC= tam giác DCH ( c-g-c)
Nên góc ACH= góc DHC
Mà hai góc này ở vị trí so le trong
Suy ra AC//HD
Lại có HK//AC ( cùng vuông góc với AB)
Vậy K, H, D thẳng hàng

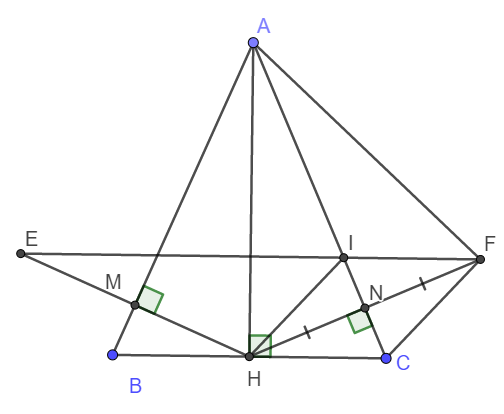
a) Do ABC là tam giác cân tại A nên AH là đường cao hay đồng thời là đường phân giác.
Xét tam giác vuông AMH và tam giác vuông ANH có:
Cạnh AH chung
\(\widehat{MAH}=\widehat{NAH}\)
\(\Rightarrow\Delta AMH=\Delta ANH\) (Cạnh huyền - góc nhọn)
\(\Rightarrow HM=HN.\)
b) Dễ dàng thấy ngay AC là đường trung trực của HF.
Khi đó thì AH = AF; CH = CF
Xét tam giác AHC và tam giác AFC có:
Cạnh AC chung
AH - AF
CH = CF
\(\Rightarrow\Delta AHC=\Delta AFC\left(c-c-c\right)\)
\(\Rightarrow\widehat{AFC}=\widehat{AHC}=90^o\Rightarrow AF\perp CF.\)
c) Ta thấy ngay \(\Delta HIN=\Delta FCN\left(g-c-g\right)\)
\(\Rightarrow IN=CN\)
Xét tam giác vuông INF và tam giác vuông CNH có:
HN = FN
IN = CN
\(\Rightarrow\Delta INF=\Delta CNH\) (Hai cạnh góc vuông)
\(\Rightarrow\widehat{IFN}=\widehat{CHN}\)
Mà chúng lại ở vị trí so le trong nên IF // BC.
d) Chứng minh tương tự câu c, ta có IE // BC
Vậy thì qua I có hai tia IE và IF cùng song song với BC nên chúng trùng nhau.
Vậy I, E, F thẳng hàng.

Hình bạn tự vẽ nhé ![]()
a) Xét ΔABM và ΔACM có:
AB=AC (gt)
AM là cạnh chung
BM=CN (M là trung điểm của BC)
=> ΔABM=ΔACM (c-c-c)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 góc tương ứng)
Mà ta có: \(\widehat{AMB}+\widehat{AMC}=90^o\)
=> \(\widehat{AMB}+\widehat{AMB}=180^o\)
=> \(\widehat{AMB}=90^o\)
=> AM vuông góc với BC
b) Theo câu a ta có: ΔABM=ΔACMB
=> \(\widehat{ABM}=\widehat{ACM}\)
Mà: \(\widehat{ABD}=180^o-\widehat{ABM}=180^o-\widehat{ACM}=\widehat{ACE}\)
Xét ΔABD và ΔACE có:
AB=AC (gt)
\(\widehat{ABD}=\widehat{ACE}\) (chứng minh trên)
BD=CE (gt)
=> ΔABD=ΔACE (c-g-c)
=> \(\widehat{BAD}=\widehat{CAE}\) (2 góc tương ứng)
Cũng theo câu a thì ΔABM=ΔACM
=> \(\widehat{BAM}=\widehat{CAM}\)
=> \(\widehat{BAM}+\widehat{BAD}=\widehat{CAM}+\widehat{CAE}\)
=> \(\widehat{DAM}=\widehat{EAM}\)
=> AM là tia phân giác của góc DAE

a, xét tam giác AMB và tam giác AMC có : AM chung
BM = CM do M là trung điểm của BC (gt)
AB = AC (gt)
=> tam giác AMB = tam giác AMC (c-c-c)
=> góc AMB = góc AMC (đn)
mà góc AMB + góc AMC = 180 (kb)
=> góc AMB = 90
=> AM _|_ BC (đn)
b, góc ABC = góc ACB do tam giác ABC cân tại A (gt)
góc ABC + góc ABD = 180 (kb)
góc ACB + góc ACE = 180 (kb)
=> góc ABD = góc ACE
xét tam giác ABD và tam giác ACE có : BD = CE (gt)
AB = AC (gt)
=> tam giác ABD = tam giác ACE (c-g-c)
Bạn tự vẽ hình nha!
a) Xét tam giác AKM và tg AHM có:
AM là cạnh chung
góc AMK= gocsAMH (=90*)
KM=HM (gt)
=> tg AKM= tg AHM (c.g.c)
=>AK=AH (cạnh tương ứng) (1)
b) Tương tự : tg AHN= tgAIN (c.g.c)
=>AH=AI (cạnh tương ứng) (2)
Từ (1) và (2) => AK=AI
Mà AK+ AI= KI
=> AK=1/2 KI
=>A là trung điểm của KI
c) Xét tg AKB và tg AHB có:
AB là cạnh chung
AK=AH (theo 1)
góc KAB= góc HAB (do tg AKM= tg AHM)
=> tg AKB= tg AHB (c.g.c)
d) cái này mik chưa bt nha