Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

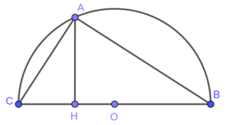
Kẻ đường cao AH (H thuộc BC) => BH/CH=9/16
=> BH=[5:(9+16)]x9=1,8 cm => CH=5-1,8=3,2 cm
\(AH^2=BH.CH=1,8.3,2=5,76\Rightarrow AH=2,4cm\)
\(S_{ABC}=\frac{BC.AH}{2}=\frac{5.2,4}{2}=6cm^2\)

Hình bài này đơn giản, bạn tự vẽ.
Kẻ đường cao AH. Theo đề bài ta có:
\(\left\{{}\begin{matrix}\dfrac{BH}{CH}=\dfrac{9}{16}\\BH+CH=BC=5\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{9}{5}\\CH=\dfrac{16}{5}\end{matrix}\right.\)
Do đó:
\(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot\sqrt{BH\cdot CH}\cdot5=...\)

Tam giác ABC vuông tại A áp dụng đính lý cạnh góc vuông và hình chiếu ta có::
\(AB^2=BC\cdot HB=BC\cdot\left(BC-HC\right)\)
\(\Rightarrow20^2=BC^2-BC\cdot9\)
\(\Rightarrow BC^2-9BC-400=0\)
\(\Rightarrow BC^2+16BC-25BC-400=0\)
\(\Rightarrow BC\left(BC+16\right)-25\left(BC+16\right)=0\)
\(\Rightarrow\left(BC+16\right)\left(BC-25\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}BC+16=0\\BC-25=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}BC=-16\left(ktm\right)\\BC=25\left(tm\right)\end{matrix}\right.\)
Áp dụng hệ thức đường cao và hình chiếu ta có:
\(AH^2=HC\cdot HB\Rightarrow AH=\sqrt{HC\cdot\left(BC-HC\right)}\)
\(\Rightarrow AH=\sqrt{9\cdot\left(25-9\right)}=12\left(cm\right)\)
Diện tích của tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot BC\cdot AH=\dfrac{1}{2}\cdot25\cdot12=150\left(cm^2\right)\)

cho tam giác ABC vuông tại A .Biết AB=7cm và AC=21 cm .tính các tỉ số lượng giác của góc B vá góc C

Bài 3:
Ta có:
\(\widehat{M}+\widehat{N}+\widehat{P}=180^o\)
\(\Rightarrow\widehat{P}=180^o-90^o-37^o=53^o\)
Mà: \(sinN=\dfrac{MN}{NP}\)
\(\Rightarrow sin37^o=\dfrac{MN}{25}\)
\(\Rightarrow MN=25\cdot sin37^o\approx15\left(cm\right)\)
Áp dung định lý Py-ta-go ta có:
\(MP=\sqrt{NP^2-MN^2}=\sqrt{25^2-15^2}=20\left(cm\right)\)
3:
a: Xét ΔABC có AC^2=BA^2+BC^2
nên ΔBAC vuông tại B
b: Xét ΔBAC vuông tại B có
sin A=BC/AC=42/58=21/29
cos A=AB/AC=40/58=20/29
tan A=BC/BA=21/20
cot A=BA/BC=20/21
c: Xét ΔABC vuông tại B có BH là đường cao
nên BH*AC=BA*BC; BA^2=AH*AC; CB^2=CH*CA
=>BH*58=40*42=1680
=>BH=840/29(cm)
BA^2=AH*AC
=>AH=BA^2/AC=40^2/58=800/29cm
CB^2=CH*CA
=>CH=CB^2/CA=42^2/58=882/29(cm)
ΔBHA vuông tại H có HE là đường cao
nênBE*BA=BH^2
=>BE*40=(840/29)^2
=>BE=17640/841(cm)
ΔBHC vuông tại H có HF là đường cao
nênBF*BC=BH^2
=>BF*42=(840/29)^2
=>BF=16800/841(cm)
Xét tứ giác BEHF có
góc BEH=góc BFH=góc EBF=90 độ
=>BEHF là hình chữ nhật
=>góc BFE=góc BHE(=1/2*sđ cung BE)
=>góc BFE=góc BAC
Xét ΔBFE và ΔBAC có
góc BFE=góc BAC
góc FBE chung
Do đó: ΔBFE đồng dạng với ΔBAC
=>S BFE/S BAC=(BF/BA)^2=(16800/441:40)^2=(420/841)^2
=>S AECF=S ABC*(1-(420/841)^2)
=>\(S_{AECF}=\dfrac{1}{2}\cdot40\cdot42\cdot\left[1-\left(\dfrac{420}{841}\right)^2\right]\simeq630,5\left(cm^2\right)\)

\(\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow AB=\dfrac{3}{4}AC\)
Áp dụng PTG
\(AB^2+AC^2=\dfrac{9}{16}AC^2+AC^2=BC^2=400\\ \Rightarrow\dfrac{25}{16}AC^2=400\\ \Rightarrow AC^2=256\\ \Rightarrow AC=16\left(cm\right)\\ \Rightarrow AB=12\left(cm\right)\\ \Rightarrow S_{ABC}=\dfrac{1}{2}AB\cdot AC=96\left(cm^2\right)\)