Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì ABDC là hình chữ nhật nên SABDC = AC. AB
mà SABC = A C . A B 2 nên SABCD = 2SABC
= 2.140 = 280 cm2.
Đáp án cần chọn là: B

a)
Ta có: HE=HA(gt)
mà A,H,E thẳng hàng
nên H là trung điểm của AE
Xét ΔAED có
H là trung điểm của AE(cmt)
M là trung điểm của AD(A và D đối xứng nhau qua M)
Do đó: HM là đường trung bình của ΔAED(Định nghĩa đường trung bình của tam giác)
⇒HM//ED và \(HM=\dfrac{1}{2}\cdot ED\)(Định lí 2 về đường trung bình của tam giác)
b) Xét tứ giác ABDC có
M là trung điểm của đường chéo BC(gt)
M là trung điểm của đường chéo AD(A và D đối xứng nhau qua M)
Do đó: ABDC là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Hình bình hành ABDC có \(\widehat{BAC}=90^0\)(ΔABC vuông tại A)
nên ABDC là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)

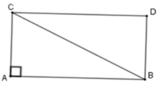
a: Xét ΔCAD vuông tại C và ΔABC vuông tại A có
góc CAD=góc ABC
=>ΔCAD đồng dạng với ΔABC
=>CA/AB=CD/AC
=>AC^2=AB*CD
b: Xét tứ giác ABDC có
AB//DC
góc CAB=90 độ
=>ABDC là hình thang vuông
c: AC^2=AB*DC
=>DC=6^2/8=4,5cm
S ABDC=1/2(AB+CD)*AC=1/2*6*(8+4,5)=12,5*3=37.5cm2

a, Ta có: DE//BC \(\Rightarrow\widehat{DEB}+\widehat{EBF}=180\)
mà góc EBF =90 => góc DEB =90 (1)
Chứng minh tương tự với DF//AB
\(\Rightarrow\widehat{EDF}=90;\widehat{BFD}=90\) (2)
Từ (1) và (2) => tứ giác BEDF là hình chữ nhật
a) vì ED//BC và DF//AB
Mà \(\Delta ABC\)vuông tại B
Nên \(DE\perp AB\)và \(DF\perp BC\)
Xét tứ giác BEDF có:
\(\widehat{B}=\widehat{DEB}=\widehat{DFB}=90^0\)
Vậy tứ giác BEDF là hình chữ nhật
Vì ABDC là hình chữ nhật nên SABDC = AC. AB
mà SABC = A C . A B 2 nên SABCD = 2SABC
= 2.55 = 110 cm2.
Đáp án cần chọn là: A
là : A nhé