Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔBAK có BA=BK
nên ΔBAK cân tại B
b: góc BAH+góc B=90 độ
góc ACB+góc B=90 độ
=>góc BAH=góc ACB
góc HAK+góc BKA=90 độ
góc KAI+góc BAK=90 độ
mà góc BKA=góc BAK
nên góc HAK=góc KAI
d: (AH+BC)^2=AH^2+2*AH*BC+BC^2
=AH^2+2*AB*AC+AB^2+AC^2
=AH^2+(AB+AC)^2>(AB+AC)^2
=>AH+BC>AB+AC
c: AH+BC>AB+AC
=>BC-AB>AC-AH
`a)`
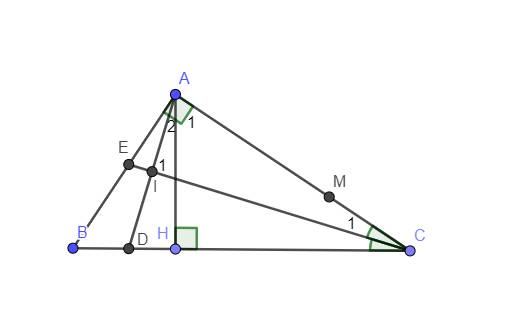
`Delta HAC` vuông tại `H` có :`hat(A_1)+hat(ACB)=90^0`
`hat(HAB)+hat(A_1)=90^0(kề bù)`
nên `hat(ACB)=hat(A_1)(đpcm)`
`b)`
`Delta HAC` vuông tại `H` có : `hat(A_1)+hat(ACH)=90^0`
hay `hat(A_1)+hat(ACB)=90^0`
`Delta ABC` vuông tại `A` có : `hat(B)=hat(ACB)=90^0`
nên `hat(B)=hat(A_1)`
Có `hat(IAC)=hat(A_1)+hat(A_2)`
`=1/2 hat(BAH)+hat(B)=1/2 hat(BCA) +hat(BAH)` (1)
`hat(C_1)=1/2 hat(ACB)(CI` là p/g của `hat(ACB)` `)`(2)
Từ `(1)` và `(2)=>hat(IAC)+hat(C_1)=hat(ABH)+hat(ACB)`
mà `hat(ABH)+hat(ACB)=90^0`
nên `hat(IAC)+hat(C_1)=90^0`
hay `hat(I_1)=90^0`
a) Ta có bd = ba (do đường cao ah là đường cao của tam giác vuông abc), và bd = ba nên tam giác abd là tam giác cân tại b.
Do đó, ad là đường phân giác của góc hacb (do ad là đường phân giác của tam giác abd).
b) Vẽ dk vuông góc với ac tại k. Ta cần chứng minh ak = ah.
Ta có tam giác akd vuông tại k, và tam giác ahd vuông tại h.
Do đó, ta cần chứng minh tam giác akd đồng dạng với tam giác ahd.
Ta có:
- Góc akd = góc ahd (vuông góc với ac)
- Góc kda = góc hda (cùng là góc nhọn)
- Cạnh ad chung
Do đó, tam giác akd đồng dạng với tam giác ahd.
Vậy, ak = ah.
c) Ta cần chứng minh ab + ac < bc + ah.
Ta có:
ab + ac = ab + ad + dc (do ad là tia phân giác của góc hacb)
= ab + ak + kc (do ak = ah và dk vuông góc với ac)
= ab + ah + kc (do ak = ah)
= ab + ah + hc (do kc = hc)
= ab + ah + bc (do ah là đường cao của tam giác abc)
= bc + ah + ab
= bc + ah + ba (do ab = ba)
= bc + ah.
Vậy, ab + ac < bc + ah.
1. Vì AB=AH(gt)
AH=AI(gt)
=> AB+AI( áp dụng tính chất bắc cầu
2. Dễ thấy góc BAH=góc BCA vì cả hai góc cùng phụ với góc ABC:
góc BAH+gócHBA=90 độ (tam giác ABH vuông tại H)
góc BCA = góc ABC = 90 độ ( tam giác ABC vuông tại A)