Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔCAP có \(\widehat{CPB}\) là góc ngoài tại đỉnh P
nên \(\widehat{CPB}=\widehat{PAC}+\widehat{PCA}=90^0+\widehat{PCA}>90^0\)
Xét ΔCPB có \(\widehat{CPB}>90^0\)
mà CB là cạnh đối diện của góc CPB
nên CB là cạnh lớn nhất trong ΔCPB
=>CB>PB
Xét ΔACB có CP là phân giác
nên \(\dfrac{AP}{AC}=\dfrac{BP}{BC}\)
mà BP<BC
nên AP<AC
b: ta có: CB là cạnh lớn nhất trong ΔCPB
=>CP<CB

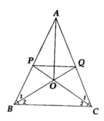
a: Xét ΔOBC có góc OBC=góc OCB
nên ΔOBC cân tại O
b: AB=AC
BO=CO
=>AO là trung trực của BC
=>AO vuông góc BC
c: Xét ΔAQB và ΔAPC có
góc ABQ=góc ACP
AB=AC
góc A chung
=>ΔAQB=ΔAPC
=>QB=PC

a/
Xét 2 tg vuông ACE và tg vuông DCE có
CE chung
\(\widehat{ACE}=\widehat{DCE}\) (gt)
=> tg ACE = tg DCE (Hai tg vuông có cạnh huyền và góc nhọn tương ứng bằng nhau)
\(\Rightarrow\widehat{AEC}=\widehat{DEC}\) => CE là phân giác \(\widehat{AED}\)
b/
Gọi M là giao của CE và AD
Ta có tg ACE = tg DCE (cmt) => AC=DC
Xét tg ACM và tg DCM có
AC=DC; CM chung
\(\widehat{ACM}=\widehat{DCM}\)
=> tg ACM = tg DCM (c.g.c) => MA=MD (1)
\(\Rightarrow\widehat{AMC}=\widehat{DMC}=\dfrac{\widehat{AMD}}{2}=\dfrac{180^o}{2}=90^o\)
\(\Rightarrow CE\perp AD\) (2)
Từ (1) và (2) => CE là đường trung trực của AD

2: Xét tứ giác ABDE có
C là trung điểm của BE
C là trung điểm của AD
Do đó: ABDE là hình bình hành
Suy ra: AB//DE

a: Xét ΔBCD vuông tại C và ΔBMD vuông tại M có
BD chung
\(\widehat{CBD}=\widehat{MBD}\)
Do đó: ΔBCD=ΔBMD
b: Ta có: ΔBCD=ΔBMD
=>BC=BM và DC=DM
Xét ΔBCM có BC=BM và \(\widehat{CBM}=60^0\)
nên ΔBCM đều
Ta có: BD là phân giác của góc CBA
=>\(\widehat{CBD}=\widehat{DBA}=\dfrac{\widehat{CBA}}{2}=\dfrac{60^0}{2}=30^0\)
Ta có: ΔBCA vuông tại C
=>\(\widehat{CBA}+\widehat{CAB}=90^0\)
=>\(\widehat{CAB}=90^0-60^0=30^0\)
Xét ΔDBA có \(\widehat{DAB}=\widehat{DBA}\left(=30^0\right)\)
nên ΔDAB cân tại D
c: Xét ΔDCK vuông tại C và ΔDMA vuông tại M có
DC=DM
CK=MA
Do đó: ΔDCK=ΔDMA
=>DK=DA
=>ΔDKA cân tại D
Ta có: BC+CK=BK
BM+MA=BA
mà BC=BM và CK=MA
nên BK=BA
=>ΔBKA cân tại B



tham khảo