Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A C B N D E M
( Thông cảm hình bị lệch )
a) + Xét \(\Delta ABC\)và \(\Delta DMC\)có :
AM = DM ( gt )
\(\widehat{AMB}=\widehat{DMC}\)( vì là hai góc đối đỉnh ) => \(\Delta AMB=\Delta DMC\)
MB = MC ( AM là trung tuyến của \(\Delta ABC\))
=> \(\widehat{B}=\widehat{MCD}\)( hai góc tương ứng )
=> DC // AB ( có hai góc so le trong = )
Mà AB \(\perp\)AC ( Vì \(\Delta ABC\)vuông tại A)
=> DC _|_ AC
+ Xét \(\Delta BEC\)có :
M là trung điểm của cạnh BC ( Vì AM là trung tuyến của ABC )
=> EM là trung tuyến
A là trung điểm của BE ( Vì EA = AB ) => CA là trung tuyến
Mà EM cắt AC tại N => N là trọng tâm của \(\Delta ABC\)
\(\Rightarrow NC=\frac{2}{3}CA\Rightarrow NC=2NA\)
+ Ta có \(\Delta AMB=\Delta DMC\Rightarrow AB=CD\)
Xét \(\Delta ACD\)có :
CD + AC > AD ( bđt tam giác ) . Mà CD = AB ; AD = 2AM
=> \(AB+AC>2AM\Leftrightarrow\frac{AB+AC}{2}>AM\)(1)
+ Xét \(\Delta AMB\)có : AM > AB - BM
\(\Delta AMC\)có : AM > AC - CM
=> 2AM > AB + AC - BM - CM
<=> 2AM > AB + AC - (BM +CM )
<=> 2AM > AB + AC - BC
<=> AM > \(\frac{AB+AC-BC}{2}\)(2)
Từ (1), (2) => Điều cần cm trên đề bài .

A B C D M 1 2 1 1
a, Xét \(\Delta MAB-\Delta MDC:\)
\(\widehat{M_1}=\widehat{M_2}\)
\(AM=MD\left(gt\right)\)
\(BM=MC\left(gt\right)\)
\(\Rightarrow\)\(\Delta MAB=\Delta MDC\left(c.g.c\right)\)
b, Có \(\Delta MAB=\Delta MDC\left(cmt\right)\)
\(\Rightarrow\widehat{A_1}=\widehat{D_1}\)
Hay AB // CD.

Ta có hình vẽ sau:
A B C D M 1 2
GT: ΔABC ; \(\widehat{A}\) = 90o
MB = MC ; MA = MD
KL: a) ΔAMB = DMC
a) Xét ΔAMB và ΔDMC có:
MA = MD (gt)
\(\widehat{M_1}\) = \(\widehat{M_2}\) ( 2 góc đối đỉnh)
MB = MC (gt)
\(\Rightarrow\) ΔAMB = ΔDMC ( cạnh - góc-cạnh)

a) Xét \(\Delta AMB\)và \(\Delta DMC\)có:
AM = MD (gt)
\(\widehat{AMB}=\widehat{DMC}\)(2 góc đối đỉnh)
MB = MC (M là trung điểm của BC)
\(\Rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\)
b) Ta có: \(\Delta AMB=\Delta DMC\)(theo a)
\(\Rightarrow\widehat{BAM}=\widehat{CDM}\)(2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong
\(\Rightarrow AB//CD\)
c) Xét \(\Delta AMB\)và \(\Delta AMC\)có:
AB = AC (gt)
AM là cạnh chung
MB = MC (M là trung điểm của BC)
\(\Rightarrow\Delta AMB=\Delta AMC\left(c.c.c\right)\)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}\)(2 góc tương ứng)
Mà \(\widehat{AMB}+\widehat{AMC}=180^o\)(2 góc kề bù)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=\frac{180^o}{2}=90^o\)
\(\Rightarrow AM\perp BC\)
d) Mk ko hiểu đề bài cho lắm!!!!!
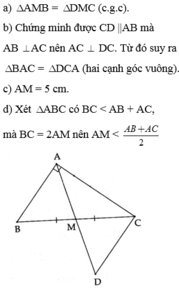

\(a)\)
Vì \(AM\)là đường trung tuyến
\(\rightarrow BM=CM\)
Xét \(\Delta AMB\)và \(\Delta DMC\)ta có:
\(\hept{\begin{cases}BM=CM\left(cmt\right)\\MD=MA\left(GT\right)\\\widehat{BMA}=\widehat{DMC}\end{cases}}\)
\(\rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\)
\(b)\)
Vì \(\Delta AMB=\Delta DMC\left(cmt\right)\)
\(\rightarrow\hept{\begin{cases}\widehat{ABM}=\widehat{MCD}\\AB=CD\end{cases}}\)
Mà hai góc này ở vị trí so le trong
\(\rightarrow AB//CD\)
Mà \(AB\perp AC\)( vì \(\Delta ABC\)vuông tại \(A\))
\(\rightarrow CD\perp AC\)
Xét \(\Delta ABC\)và \(DCM\)ta có:
\(\hept{\begin{cases}AB=CD\left(cmt\right)\left(cmt\right)\\ACchung\\\widehat{BAC}=\widehat{DCA}=90^o\end{cases}}\)
\(\rightarrow\Delta ABC=\Delta DMC\left(c.g.c\right)\)
\(c)\)
Ta có: \(AB=DC=6cm\)
Xét \(\Delta DCA\)vuông tại \(C\)ta có:
\(DC^2+AC^2=AD^2\)
\(\rightarrow AD^2=6^2+8^2\)
\(\rightarrow AD^2=10^2\)
\(\rightarrow AD=10cm\)
Mà \(MD=MA\)
\(\rightarrow M\)là trung điểm của \(AD\)
\(\rightarrow AM=\frac{1}{2}AD=\frac{1}{2}.10=5cm\)
\(d)\)
Giả sử: \(AM< \frac{AB+AC}{2}\)
Ta có: \(\frac{AB+AC}{2}=\frac{6+8}{2}=\frac{14}{2}=7cm\)
Mà \(AM=5cm\)
\(\rightarrow5cm< 7cm\)
\(\rightarrow AM< \frac{AB+AC}{2}\)
M C A B D