Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài làm
a) Xét tam ABC vuông tại A có:
\(\widehat{ACB}+\widehat{ABC}=90^0\)( hai góc phụ nhau )
hay \(\widehat{ACB}+60^0=90^0\)
=> \(\widehat{ACB}=90^0-60^0=30^0\)
b) Xét tam giác ABE và tam giác DBE có:
\(\widehat{BAE}=\widehat{BDE}=90^0\)
Cạnh huyền: BE chung
Cạnh góc vuông: AB = BD ( gt )
=> Tam giác ABE = tam giác DBE ( cạnh huyền - cạnh góc vuông )
=> \(\widehat{ABE}=\widehat{DBE}\)( hai góc tương ứng )
=> BI là tia phân giác của góc BAC
Mà I thược BE
=> BE là tia phân giác của góc BAC
Gọi I là giao điểm BE và AD
Xét tam giác AIB và tam giác DIB có:
AB = BD ( gt )
\(\widehat{ABE}=\widehat{DBE}\)( cmt )
BI chung
=> Tam giác AIB = tam giác DIB ( c.g.c )
=> AI = ID (1)
=> \(\widehat{BIA}=\widehat{BID}\)
Ta có: \(\widehat{BIA}+\widehat{BID}=180^0\)( hai góc kề bù )
Hay \(\widehat{BIA}=\widehat{BID}=\frac{180^0}{2}=90^0\)
=> BI vuông góc với AD tại I (2)
Từ (1) và (2) => BI là đường trung trực của đoạn AD
Mà I thược BE
=> BE là đường trung trực của đoạn AD ( đpcm )
c) Vì tam giác ABE = tam giác DBE ( cmt )
=> AE = ED ( hai cạnh tương ứng )
Xét tam giác AEF và tam giác DEC có:
\(\widehat{EAF}=\widehat{EDC}=90^0\)
AE = ED ( cmt )
\(\widehat{AEF}=\widehat{DEF}\)( hai góc đối )
=> Tam giác AEF = tam giác DEC ( g.c.g )
=> AF = DC
Ta có: AF + AB = BF
DC + BD = BC
Mà AF = DC ( cmt )
AB = BD ( gt )
=> BF = BC
=> Tam giác BFC cân tại B
=> \(\widehat{BFC}=\widehat{BCF}=\frac{180^0-\widehat{FBC}}{2}\) (3)
Vì tam giác BAD cân tại B ( cmt )
=> \(\widehat{BAD}=\widehat{BDA}=\frac{180^0-\widehat{FBC}}{2}\) (4)
Từ (3) và (4) => \(\widehat{BAD}=\widehat{BFC}\)
Mà Hai góc này ở vị trí đồng vị
=> AD // FC
d) Xét tam giác ABC vuông tại A có:
\(\widehat{ACB}+\widehat{ABC}=90^0\)( hai góc phụ nhau ) (5)
Xét tam giác DEC vuông tại D có:
\(\widehat{DEC}+\widehat{ACB}=90^0\)( hai góc phụ nhau ) (6)
Từ (5) và (6) => \(\widehat{ABC}=\widehat{DEC}\)
Ta lại có:
\(\widehat{ABC}>\widehat{EBC}\)
=> AC > EC
Mà \(\widehat{EBC}=\frac{1}{2}\widehat{ABC}\)
=> EC = 1/2 AC.
=> E là trung điểm AC
Mà EC = EF ( do tam giác AEF = tam giác EDC )
=> EF = 1/2AC
=> AE = EC = EF
Và AE = ED ( cmt )
=> ED = EC
Mà EC = 1/2AC ( cmt )
=> ED = 1/2AC
=> 2ED = AC ( đpcm )
Mình chứng minh ra kiểu này cơ. không biết đề đúng hay sai!??

a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
b: Ta có: ΔABD=ΔAED
nên DB=DE
mà DE<DC
nên DB<DC
c: Ta có: AB=AE
DB=DE
Do đó: AD là đường trung trực của BE

Bài 1 : Bài giải
A B C H D F E
Bài 2 : Bài giải
A C B D E I F
Bài 3 : Bài giải
A B C D E 1 2 H I
Xét 2 tam giác \(\Delta ABI\text{ và }\Delta EBI\) có :
\(BA=BE\) ( gt )
\(BD\) : cạnh chung
\(\widehat{B_1}=\widehat{B_2}\) ( BD là đường phân giác của \(\widehat{B}\) )
\(\Rightarrow\text{ }\Delta ABD=\Delta EBD\text{ }\left(c.g.c\right)\)
\(\Rightarrow\text{ }AD=DE\text{ }\left(2\text{ cạnh tương ứng }\right)\)
....
Tự làm tiếp nha ! Mình bận rồi !

a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
b: ta có: ΔABD=ΔEBD
nên DA=DE
mà BA=BE
nên BD là đường trung trực của AE
hay BD⊥AE
mình không biết vẽ hình nên bạn tự vẽ nha
a) có :BD là tia phân giác của góc ABC
=> góc ABD = góc DBC hay góc ABD = góc DBE
xét △ABD và △EBD có :
AB=EB
góc ABD = góc DBE
DB là cạnh chung
=> △ABD=△EBD(c.g.c)
b) có : △ABD=△EBD => AD=ED
=>D ∈ đường trung trực của EA
có AB=EB => B thuộc đường trung trực của EA
=> BD là đường trung trực của EA
=> BD⊥EA hay BH⊥EA
c) có : △ABD=△EBD => góc ADB= góc BDE(1)
có AK// BD
=> góc ADB= góc KAD(SLT)(2)
và góc AKD= góc BDE(ĐV)(3)
từ (1),(2),(3) => góc KAD= góc AKD
=> △ADK cân tại D
=> DA=DK
mà AD=DE =>DE=DK=AD
=> D là trung điểm của EK
d) có : góc BDA= góc DBC+góc C ( vì là góc ngoài) và góc ABD=góc DBC
=>góc DBA=góc ABD+góc C
=>góc DBA<góc ABD
trong △ABD có :góc DBA<góc ABD
=> AD<AB( quan hệ giữa cạnh và góc đối diện)
lại có AD=DK=DE
=> AB>DK
=>AB+AB>DK+DK
=>2AB>DK+DE
=>KE<2AB
nếu có chỗ sai mong thầy cô và các bạn trong hoc24 giúp mình sửa giúp để mình có thể giỏi hơn

a)xét tg ABD và tg CBD có:
+ AB=BE(gt)
+ góc ABD = EBD (BD là phân giác)
+BD chung
=>tg ABD= tg EBD(c.gc)
b) vì tg ABD=tgEBD
=> AD=DE và góc BAD = BED (=90 độ)
=> DE ⊥ BC
=> tg DEC có DC là cạnh huyền =>DC>ED mà ED=AD => DC>AD
c)xét tg BFE và tg BCA có:
+ Góc E = A (=90 độ)
+góc B chung
+ BE=BA
=>tg BFE =tg BCA (gcg)
=>BF=BC
=> tg BFC cân tại B
vì S là td FC
=>BS vừa là trung tuyến vừa là đường cao
=>BS⊥FC (1)
tg BFC có: D là giao của 2 đg cao CA và FE
=> D là trực tâm => BD ⊥ FC (2)
từ 1 và 2 => B,D,S thẳng hàng
Sửa đề: AB = BE (không phải AB = AE)
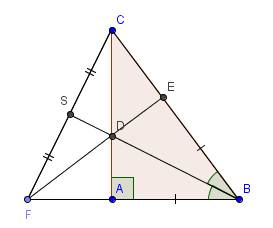
Gởi hình vẽ trước, đi công việc, tí sửa sau

4:
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
c: AE=AF
ME=MF
=>AM là trung trực của EF
mà K nằm trên trung trực của EF
nên A,M,K thẳng hàng
a, Xét ΔABD và ΔEBD có :
BD là cạnh chung
góc ABD = góc EBD (BD là tia phân giác của góc ABE)
BA = BE (gt)
=> ΔABD = ΔEBD (c.g.c)
=> AD = ED (2 cạnh tương ứng)