Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Áp dụng định lí Pytago vào ΔAHB vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow AH^2=13^2-5^2=144\)
hay AH=12(cm)
Xét ΔABH vuông tại H có
\(\sin\widehat{B}=\dfrac{AH}{AB}=\dfrac{12}{13}\)
\(\Leftrightarrow\cos\widehat{C}=\dfrac{12}{13}\)
hay \(\sin\widehat{C}=\dfrac{5}{13}\)
a) Áp dụng đlí Py - ta - go cho tam giác HAB ( ^H =90^o )
Ta có : \(AB^2=AH^2+BH^2\)
\(13^2=AH^2+5^2\)
\(AH^2=13^2-5^2\)
\(\Rightarrow AH=\sqrt{13^2-5^2}\)
\(\sin B=\frac{AH}{AB}=\frac{\sqrt{13^2-5^2}}{13}\approx0,923\)
Áp dụng hệ thức lượng cho tam giác ABC( ^A = 90^o ) , đường cao AH , ta có :
\(AH^2=BH.HC\Rightarrow HC=\frac{AH^2}{BH}=\frac{12^2}{5}=28,8\)
=> BC = 5 + 28,8 = 33,8
\(\sin C=\frac{AB}{BC}=\frac{13}{33,8}\approx0,384\)
Vậy : \(\sin B\approx0,923\)
\(\sin C\approx0,384\)
a, Áp dụng các tỉ số lượng giác cho tam giác vuông ABH để tính sinB, rồi từ đó suy ra sinC
b, Áp dụng hệ thức lượng về cạnh góc vuông và hình chiếu lên cạnh huyền trong tam giác vuông ABC để tính AB. Sau đó làm tương tự câu a)
a: AH=căn 13^2-5^2=12
Xét ΔAHB vuông tại H có
sin B=AH/AB=12/13=cos C
cos B=sin C=BH/AB=5/13
tan B=cot C=AH/BH=12/5
cot B=tan C=BH/AH=5/12
b: AH=căn 3*4=2*căn 3(cm)
BC=3+4=7(cm)
AB=căn 3*7=căn 21(cm)
AC=căn 4*7=2*căn 7(cm)
Xét ΔABC vuông tại A có
sin B=cos C=AC/BC=2*căn 7/7
cos B=sin C=AB/BC=căn 21/7
tan B=cot C=2*căn 7/căn 21=2/căn 3
cot B=tan C=căn 21/2*căn 7=căn 3/2
AH=căn 3*4=2căn 3(cm)
AB=căn 3*7=căn 21(cm)
AC=căn 4*7=căn 28(cm)
sin B=AC/BC=căn 28/7=0,7559
sin C=AB/BC=căn 21/7=0,6547
a) Xét ΔAHB có ^AHB = 900 ( AH ⊥ BC ) => ΔAHB vuông tại H
Khi đó : \(\sin B=\sin\widehat{ABH}=\frac{AH}{AB}=\frac{5}{13};\cos B=\cos\widehat{ABH}=\frac{BH}{AB}=\frac{\sqrt{AB^2-AH^2}\left(pythagoras\right)}{AB}=\frac{12}{13}\)
ΔABC vuông tại A => ^B + ^C = 900 => \(\sin C=\cos B=\frac{12}{13}\)
b) Áp dụng hệ thức lượng trong tam giác vuông cho ΔABC vuông tại A ta có :
\(AH^2=BH\cdot HC\Rightarrow AH=\sqrt{BH\cdot HC}=2\sqrt{3}\)
cmtt như a) ta có được ΔAHC vuông tại H
Khi đó : \(\sin C=\sin\widehat{ACH}=\frac{AH}{AC}=\frac{AH}{\sqrt{AH^2+HC^2}}=\frac{\sqrt{21}}{7};\cos C=\cos\widehat{ACH}=\frac{CH}{AC}=\frac{CH}{\sqrt{AH^2+HC^2}}=\frac{2\sqrt{7}}{7}\)ΔABC vuông tại A => ^B + ^C = 900 => \(\sin B=\cos C=\frac{2\sqrt{7}}{7}\)
a)
xét tam giác ABH vuông tại H có:
\(AH^2=AB^2-BH^2\Rightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{13^2-5^2}=12\)
theo tỉ lệ thức trong tam giác vuông ABC có:
\(AH^2=BH.CH\Rightarrow HC=\frac{AH^2}{BH}=\frac{12^2}{5}=\frac{144}{5}=28,8\)
xét tam giác vuông AHC có:
\(AC^2=AH^2+HC^2\Rightarrow AC=\sqrt{AH^2+HC^2}=\sqrt{12^2+28,8^2}=\frac{156}{5}=31,2\)
vậy : \(\sin B=\frac{AH}{AB}=\frac{12}{13}\)
\(\sin C=\frac{AH}{AC}=\frac{12}{31,2}=\frac{5}{13}\)
b)
theo tỉ số lượng giác trong tam giác ABC có:
\(AH^2=BH.CH\Rightarrow AH=\sqrt{BH.CH}=\sqrt{3.4}=2\sqrt{3}\)
xét tam giác vuông ABH có:
\(AB^2=AH^2+BH^2\Rightarrow AB=\sqrt{AH^2+BH^2}=\sqrt{\left(2\sqrt{3}\right)^2+3^2}=\sqrt{21}\)
theo hệ thức lượng trong tam giác vuông ABC có:
\(AC^2=BC.HC\Rightarrow AC=\sqrt{BC.HC}=\sqrt{7.4}=2\sqrt{7}\)
Vậy : \(\sin B=\frac{AH}{AB}=\frac{2\sqrt{3}}{\sqrt{21}}=\frac{2\sqrt{7}}{7}\)
\(\sin C=\frac{AH}{AC}=\frac{2\sqrt{3}}{2\sqrt{7}}=\frac{\sqrt{21}}{7}\)
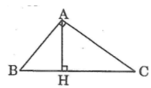
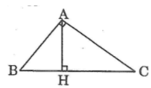
a, Áp dụng hệ thức AB^2=BH.BC
<=> 13^2=5.BC
=> BC=33,8
áp dụng định lý pytago vào tam giác ABC
AB^2+AC^2=BC^2
<=> 13^2+AC^2=33.8^2
=> AC=31,2
\(\sin B=\frac{AC}{BC}=\frac{31,2}{33,8}=\frac{12}{13}\)
\(\sin C=\frac{AB}{BC}=\frac{13}{33,8}=\frac{5}{13}\)
a) Áp dụng đlí Py - ta - go cho tam giác HAB ( \(\widehat{H}=90^o\))
Ta có : \(AB^2=AH^2+BH^2\)
\(13^2=AH^2+5^2\)
\(AH^2=13^2-5^2\)
\(\Leftrightarrow AH=\sqrt{13^2-5^2}\)
\(\sin B=\frac{AH}{AB}=\frac{\sqrt{13^2-5^2}}{13}\approx0,923\)
Áp dụng hệ thức lượng cho tam giác ABC ( \(\widehat{A}=90^o\)) , đường cao AH , ta có :
\(AH^2=BH.HC\Rightarrow HC=\frac{HC^2}{BH}=\frac{12^2}{5}=28,8\)
\(\Rightarrow BC=5+28,8=33,8\)
\(\sin C=\frac{AB}{BC}=\frac{13}{33,8}\approx0,384\)
Vậy : \(\sin B\approx0,923\)
\(\sin C\approx0,384\)