Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn kham khảo link này nhé.
Câu hỏi của Đào Gia Khanh - Toán lớp 7 - Học toán với OnlineMath
đề bài bn cho sai đấy nhé,chỗ "gọi E là giao điểm của ME và AB" ấy, ở đó đáng lẽ pk là F là giao điểm đúng ko? mk đã sửa lại rồi đấy.
a) ta có tam giác ABM=tam giác EBM(CH-GN)
=> AB=EB
gọi H là giao điểm của AE và MB
xét tam giác HBA và tam giác HBE có:
HB cạnh chung
\(\widehat{HBA}\)=\(\widehat{HBE}\)(gt)
AB=EB(cmt)
=> tam giác HBA=tam giác HBE(c.g.c)
=> HA=HE => H là trung điểm của AE(1)
\(\widehat{AHB}\)=\(\widehat{EHB}\)mà 2 góc này ở vị trí kề bù nên \(\widehat{AHB}\)=\(\widehat{EHB}\)=90 độ
=> BH\(\perp\)AE(1)
từ (1) và (2) suy ra BM là trung trực của AE
b) xet 2 tam giác vuông AMF và EMC có:
AM=ME(vì t.giác ABM=t.giác EBM)
\(\widehat{AMF}\)=\(\widehat{EMC}\)(vì đối đỉnh)
=> tam giác AMF=tam giác EMC(cạnh góc vuông-góc nhọn kề)
=> MC=MF(2 cạnh tương ứng)

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=5^2-3^2=16\)
=>\(AC=\sqrt{16}=4\left(cm\right)\)
b: Sửa đề: ME cắt BA tại K
Xét ΔABM vuông tại A và ΔEBM vuông tại E có
BM chung
\(\widehat{ABM}=\widehat{EBM}\)
Do đó: ΔBAM=ΔBEM
c: Ta có: ΔBAM=ΔBEM
=>BA=BE
Xét ΔBEK vuông tại E và ΔBAC vuông tại A có
BE=BA
\(\widehat{EBK}\) chung
Do đó: ΔBEK=ΔBAC
=>BK=BC
=>ΔBKC cân tại B
d: Ta có: MA+MC=AC
ME+MK=KE
mà AC=KE và MA=ME
nên MK=MC
=>ΔMKC cân tại M
=>\(\widehat{KMC}=180^0-2\cdot\widehat{MKC}\)
mà \(\widehat{KMC}=\widehat{AME}\)(hai góc đối đỉnh)
nên \(\widehat{AME}=180^0-2\cdot\widehat{MKC}\left(1\right)\)
Xét tứ giác BAME có
\(\widehat{BAM}+\widehat{BEM}+\widehat{ABE}+\widehat{AME}=360^0\)
=>\(\widehat{AME}+\widehat{ABC}=180^0\)
=>\(\widehat{AME}=180^0-\widehat{ABC}\left(2\right)\)
Từ (1),(2) suy ra \(\widehat{ABC}=2\cdot\widehat{MKC}\)

a:Xét ΔCAD vuông tại A và ΔCED vuông tại E có
CD chung
góc ACD=góc ECD
=>ΔCAD=ΔCED
=>DA=DE
=>ΔDAE cân tại D
b: CA=CE
DA=DE
=>CD là trung trực của AE
=>MA=ME và CM vuông góc AE tại M

a/ Xét tam giác ABM và tam giác EBM:
+ ^A = ^AEB ( = 90o)
+ BM chung
+ ^ABM = ^EBM ( do BM là phân giác ^B)
=> Tam giác ABM = Tam giác EBM (ch - gn)
b/ Ta có: ^A = ^B + ^C = 90o (do tam giác ABC vuông tại A)
Mà ^C = 30o (gt)
=> ^B = 60o
Tam giác ABM = Tam giác EBM (cmt)
=> AB = EB (cặp cạnh tương ứng)
=> Tam giác ABE cân tại B
Lại có: ^B = 60o (cmt)
=> Tam giác ABE đều

a) Xét ΔAMB và ΔEMB có
BA=BE(gt)
\(\widehat{ABM}=\widehat{EBM}\)(BM là tia phân giác của \(\widehat{ABE}\))
BM chung
Do đó: ΔAMB=ΔEMB(c-g-c)
Suy ra: \(\widehat{MAB}=\widehat{MEB}\)(hai góc tương ứng)
mà \(\widehat{MAB}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{MEB}=90^0\)
hay ME\(\perp\)BC(đpcm)
b) Ta có: ΔABC vuông tại A(gt)
\(\Leftrightarrow\widehat{ABC}+\widehat{ACB}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{ABC}+30^0=90^0\)
\(\Leftrightarrow\widehat{ABC}=60^0\)
hay \(\widehat{ABE}=60^0\)
Xét ΔABE có BA=BE(gt)
nên ΔBAE cân tại B(Định nghĩa tam giác cân)
Xét ΔBAE cân tại B có \(\widehat{ABE}=60^0\)(cmt)
nên ΔBAE đều(Dấu hiệu nhận biết tam giác đều)

a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
\(\widehat{AOM}=\widehat{BOM}\)
Do đó: ΔOAM=ΔOBM
=>MA=MB
Xét ΔMAF vuông tại A và ΔMBE vuông tại B có
MA=MB
\(\widehat{AMF}=\widehat{BME}\)
Do đó: ΔMAF=ΔMBE
=>MF=ME
b:
Ta có: OA=OB
=>O nằm trên đường trung trực của BA(1)
Ta có: MA=MB
=>M nằm trên đường trung trực của BA(2)
Từ (1) và (2) suy ra OM là đường trung trực của BA
=>OM\(\perp\)BA



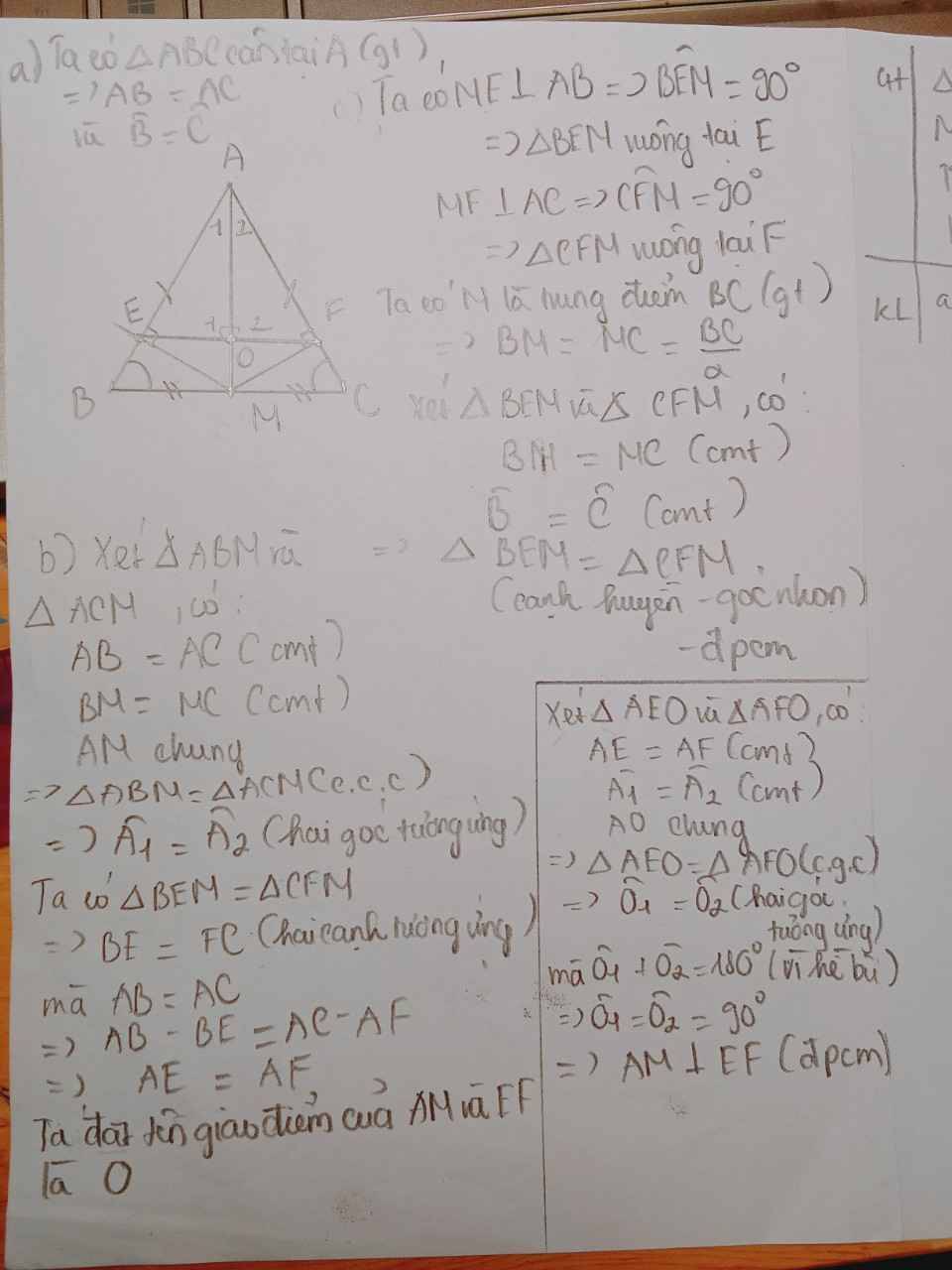
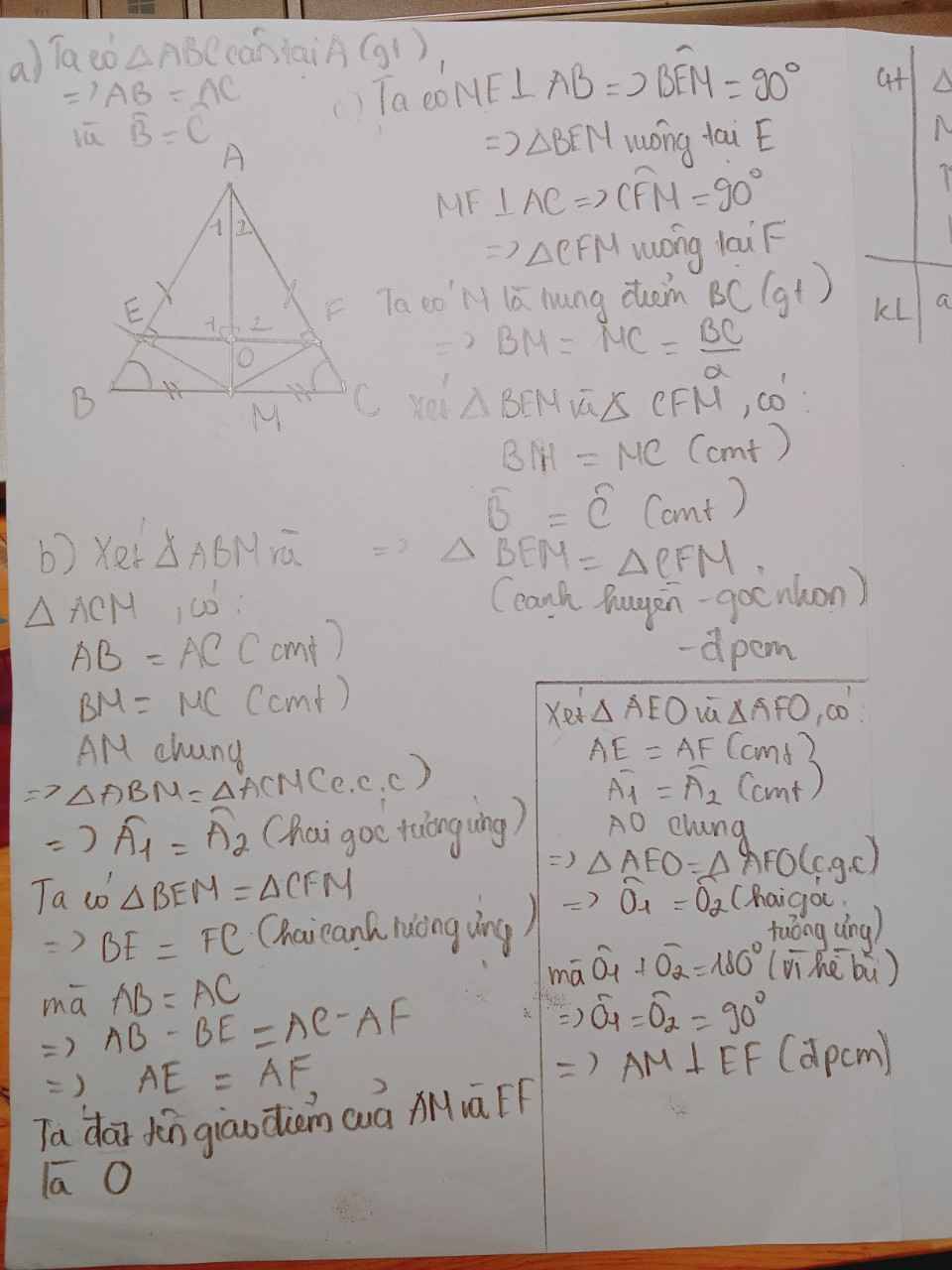
Xét ΔBAM vuông tại A và ΔBEM vuông tại E có
BM chung
góc ABM=góc EBM
=>ΔBAM=ΔBEM
=>MA=ME