Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A C A B K H I
a) Xem lại đề vì nếu bằng nhau => BA//BK vô lí
b) Xét tam giác ABK có: \(\widehat{ABK}+\widehat{BKA}+\widehat{BAK}=180^o\)
Xét tam giác BIH có: \(\widehat{IBH}+\widehat{HIB}+\widehat{IHB}=180^o\)
Mà \(\widehat{ABK}=\widehat{IBH}\)( vì BK là phân giác góc B trong tam giác ABC)
\(\widehat{BAK}=\widehat{BHI}=90^o\)
Suy ra góc BKA=góc HIB mà góc HIB =góc AIK đối đỉnh
=> Góc AIK = góc BKA= góc AKI

Có gì khong hiểu hỏi lại cj nhé:
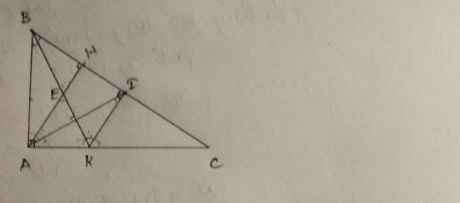
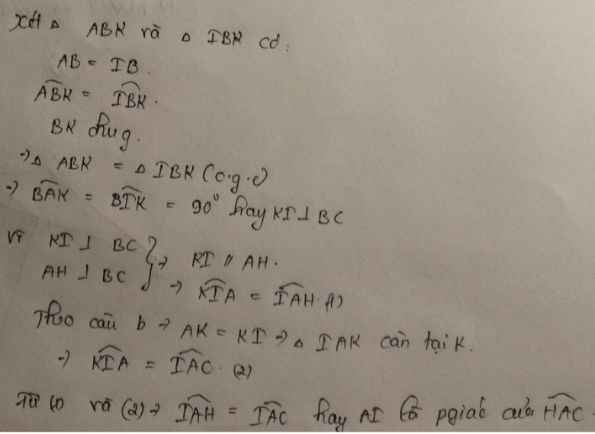
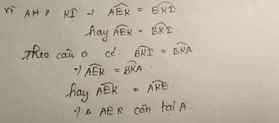
a, b ,c lần lượt từ trên xuống.

b) Ta có: KI\(\perp\)BC(gt)
AH\(\perp\)BC(gt)
Do đó: KI//AH(Định lí 1 từ vuông góc tới song song)
Suy ra: \(\widehat{HAI}=\widehat{KIA}\)(hai góc so le trong)(1)
Ta có: ΔABK=ΔIBK(cmt)
nên KA=KI(hai cạnh tương ứng)
Xét ΔKAI có KA=KI(cmt)
nên ΔKAI cân tại K(Định nghĩa tam giác cân)
Suy ra: \(\widehat{KAI}=\widehat{KIA}\)(hai góc ở đáy)(2)
Từ (1) và (2) suy ra \(\widehat{HAI}=\widehat{KAI}\)
\(\Leftrightarrow\widehat{HAI}=\widehat{CAI}\)
Suy ra: AI là tia phân giác của \(\widehat{HAC}\)(Đpcm)
a) Xét ΔABK vuông tại A và ΔIBK vuông tại I có
BK chung
\(\widehat{ABK}=\widehat{IBK}\)(BK là tia phân giác của \(\widehat{ABI}\))
Do đó: ΔABK=ΔIBK(Cạnh huyền-góc nhọn)

a) Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC(ΔABC cân tại A)
\(\widehat{KAC}\) chung
Do đó: ΔAHB=ΔAKC(cạnh huyền-góc nhọn)
⇒AH=AK(hai cạnh tương ứng)
b) Xét ΔAHK có AH=AK(cmt)
nên ΔAHK cân tại A(Định nghĩa tam giác cân)
⇒\(\widehat{AKH}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔAHK cân tại A)(1)
Ta có: ΔABC cân tại A(gt)
nên \(\widehat{ABC}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔABC cân tại A)(2)
Từ (1) và (2) suy ra \(\widehat{AKH}=\widehat{ABC}\)
mà \(\widehat{AKH}\) và \(\widehat{ABC}\) là hai góc ở vị trí đồng vị
nên HK//BC(dấu hiệu nhận biết hai đường thẳng song song)

a: Xét ΔAKB vuông tại K và ΔAFC vuông tại F có
AB=AC
góc A chung
=>ΔAKB=ΔAFC
b: Xét ΔABC có
BK,CF là đường cao
BK cắt CF tại H
=>H là trực tâm
=>AH vuông góc BC tại I
=>AI là trung trực của BC
a: \(\widehat{AIK}=180^0-\widehat{HAC}-\widehat{AKB}\)
\(=90^0-\widehat{HAC}+90^0-\widehat{AKB}\)
\(=\widehat{ABK}+\widehat{C}=\widehat{KBC}+\widehat{BAH}\)
b: \(\widehat{AKI}=90^0-\widehat{ABK}\)
\(\widehat{AIK}=\widehat{BIH}=90^0-\widehat{KBC}\)
mà \(\widehat{ABK}=\widehat{KBC}\)
nên \(\widehat{AKI}=\widehat{AIK}\)