Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) ADME là hình chữ nhật vì có 3 góc vuông: \(\widehat{A}\)= \(\widehat{D}\)= \(\widehat{E}\)= 900
b) Để ADME là hình vuông thì AM là phân giác \(\widehat{A}\)
Vậy M là giao đường phân giác góc A với BC thì ADME là hình vuông

a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
=>ADME là hình chữ nhật
b: ADME là hình chữ nhật
=>AD//EM và AD=EM(1)
M là trung điểm của EK
=>\(EK=2EM\left(2\right)\)
A là trung điểm của ID
=>\(ID=2DA\left(3\right)\)
Từ (1),(2),(3) suy ra EK=ID
EM//AD
K\(\in\)EM
I\(\in\)AD
Do đó: EK//ID
Xét tứ giác EKDI có
EK//DI
EK=DI
Do đó: EKDI là hình bình hành

DMA = MAN = AND = 900 (gt)
=> AMDN là hình chữ nhật
=> AB // ND
mà D là trung điểm của BC (gt)
=> N là trung điểm của AC
mà N là trung điểm của DE (gt)
=> ADCE là hình bình hành
mà DE _I_ AC (gt)
=> ADCE là hình thoi
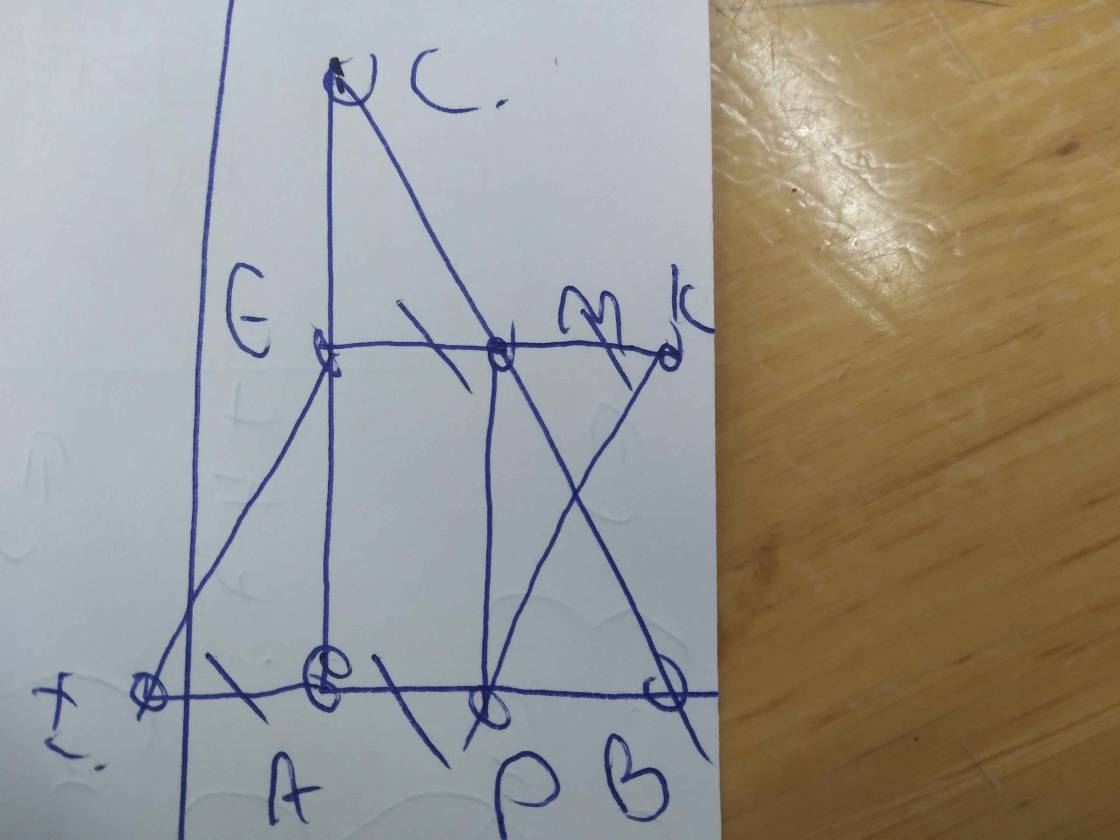


a) xét tứ giác APMN có
\(\widehat{BAC}=90^o\\ \widehat{MNA}=90^O\\ \widehat{MPA}=90^O\)
=> tứ giác APMN là hình chữ nhật
b) ΔABC vuông tại A, có đường trung tuyến AM
=> AM = MC (1)
=> ΔAMC là tam giác cân
Lại có MP là đường cao (\(\widehat{MPA}=90^O\))
=> MP cũng là đường trung tuyến
=> PA = PC
xét tứ giác AMCQ có
PM = PQ (giả thiết)
PA = PC (chứng minh trêN)
=> tứ giác AMCQ là hình bình hành (2)
từ (1) và (2) => hình bình hành AMCQ là hình thoi