Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Câu a. Chứng minh A, D, E cùng thuộc (O; OA)
Ta phân tích:
- O là tâm nội tiếp △ABC. Vậy OA, OB, OC là phân giác các góc A, B, C.
- Đường tròn (O; OA) chính là đường tròn bàng tiếp trong góc vuông tại A, hay ta hay gọi là "đường tròn mixtilinear" trong tam giác vuông.
👉 Điều cần chứng minh: D, E cũng nằm trên đường tròn này.
- Xét tam giác vuông AHB: Tia phân giác của ∠BAH đi qua D.
- Tia phân giác của ∠BAH chia ∠BAH thành 2 góc bằng nhau. Nhưng ta lại biết OA cũng là phân giác ∠BAC.
=> D nằm trên đường tròn (O; OA).
- Lập luận tương tự cho E từ tam giác vuông AHC.
Kết luận: Đường tròn (O; OA) đi qua A, D, E. ✅
Câu b. Tính số đo ∠DOE
Ta biết:
- D, E cùng nằm trên (O; OA).
- Đường tròn này đối xứng qua phân giác ∠A.
👉 Suy nghĩ: ∠DOE sẽ liên quan đến ∠BAC.
- Vì A là đỉnh góc vuông (∠A = 90°).
- D và E là ảnh của nhau qua phân giác ∠BAC (tức qua OA).
- Vậy ∠DOE = 2 × ∠BAC = 2 × 90° = 180°/2 ??? → Chờ kiểm tra kỹ.
Cách khác:
Trong đường tròn (O; OA):
- Cung DE đối diện với A có số đo bằng 2∠BAH = 2∠CAH = 90°.
- Nên ∠DOE = 90°.
✅ Kết quả:
a) (O; OA) đi qua A, D, E.
b) ∠DOE = 90°.
tham khảo
a) Chứng minh đường tròn tâm \(O\), bán kính \(O A\) đi qua \(A , D , E\)
- \(O D , O E\) lần lượt là các tia phân giác trong của \(\triangle A B C\) nên theo tính chất đường phân giác, ta suy ra \(O\) là tâm đường tròn nội tiếp tam giác \(A B C\).
- \(D\) thuộc phân giác góc \(\angle B A H\), \(E\) thuộc phân giác góc \(\angle C A H\). Với cách dựng như đề bài, ta chứng minh được:
\(\angle D A O = \angle O A E \Rightarrow O D = O E = O A .\) - Như vậy \(A , D , E\) cùng cách đều \(O\). Suy ra chúng cùng nằm trên đường tròn tâm \(O\) bán kính \(O A\).
Kết luận: Đường tròn tâm \(O\), bán kính \(O A\) đi qua 3 điểm \(A , D , E\)b) Tính số đo góc \(\hat{D O E}\)
Vì tam giác \(A B C\) vuông tại \(A\) nên:
\(\angle B A C = 90^{\circ} .\)
Theo giả thiết:
- \(D\) nằm trên phân giác của góc \(\angle B A H = \alpha\),
- \(E\) nằm trên phân giác của góc \(\angle C A H = \alpha\),
Suy ra:
\(\angle D A O = \frac{\alpha}{2} , \angle E A O = \frac{\alpha}{2} .\)
Mà:
\(\angle B A H + \angle H A C = 90^{\circ} \Rightarrow 2 \alpha = 90^{\circ} \Rightarrow \alpha = 45^{\circ} .\)
⇒
\(\angle D A O = \angle E A O = \frac{45^{\circ}}{2} = 22,5^{\circ} .\)
Trong tứ giác \(A D O E\) nội tiếp đường tròn tâm \(O\) (bán kính \(O A\)) thì cung nhỏ \(D E\) chắn góc ở tâm bằng:
\(\angle D O E = 2 \angle D A E .\)
Mà:
\(\angle D A E = \angle D A O + \angle O A E = 22,5^{\circ} + 22,5^{\circ} = 45^{\circ} .\)
Đ/s: \(\angle DOE=90^{\circ}\)
a: Xét tứ giác BFED có
ED//BF
FE//BD
Do đó: BFED là hình bình hành
Xét ΔABC có
D là trung điểm của BC
DE//AB
Do đó: E là trung điểm của AC
Xét ΔABC có
E là trung điểm của AC
EF//CB
Do đó: F là trung điểm của AB
Xét ΔCDE và ΔEFA có
CD=EF
DE=FA
CE=EA
Do đó: ΔCDE=ΔEFA
b: Gọi ΔABC có F là trung điểm của AB,E là trung điểm của AC
Trên tia FE lấy điểm E sao cho E là trung điểm của FK
Xét tứ giác AFCK có
E là trung điểm của AC
E là trung điểm của FK
Do đó: AFCK là hình bình hành
Suy ra: AF//KC và KC=AF
hay KC//FB và KC=FB
Xét tứ giác BFKC có
KC//FB
KC=FB
Do đó: BFKC là hình bình hành
Suy ra: FE//BC(ĐPCM)
4 bài toàn là hình, lại khó, dài , mk nghĩ chắc ko ai tl giúp bn đâu, xl nha, ngay mk mới lp 6 cx chưa thể giải đc vì đã lp 7 đâu. ah hay là bn gửi tg bài 1 cho các bn ấy giải từ từ, cứ 1 đốg thì ai giải giúp bn đc. sorry nha
*In đậm: quan trọng.
Câu a
Xét tam giác ABD và AMD có
AB = AM từ gt
Góc BAD = MAD vì AD phân giác BAM
AD chung
=> 2 tam guacs bằng nhau
Câu b
Ta có: Góc EMD bằng CMD vì góc ABD bằng AMD
Bd = bm vì 2 tam giác ở câu a bằng nhau
Góc BDE bằng MDC đối đỉnh
=> 2 tam giác bằng nhau
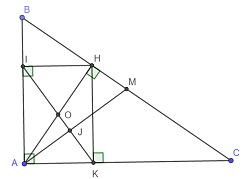
a) Xét tứ giác AIHK có \(\widehat{AIH}+\widehat{IAK}+\widehat{AKH}=270^o\Rightarrow\widehat{IHK}=90^o\)
Vậy nên \(HI\perp HK\)
b) Do IA và HK cùng vuông góc với AC nên IA // HK
Vậy thì \(\widehat{IAH}=\widehat{KHA}\) (So le trong)
Xét tam giác IAH và tam giác KHA có:
\(\widehat{AIH}=\widehat{HKA}=90^o\)
Cạnh AH chung
\(\widehat{IAH}=\widehat{KHA}\)
\(\Rightarrow\Delta AIH=\Delta HKA\) (Cạnh huyền - góc nhọn)
\(\Rightarrow IA=HK.\)
c) Xét tam giác IAH và tam giác HKI có:
\(\widehat{AIH}=\widehat{KHI}=90^o\)
Cạnh IH chung
\(IA=HK\)
\(\Rightarrow\Delta AIH=\Delta KHI\) (Hai cạnh góc vuông)
\(\Rightarrow AH=IK.\)
d) Ta thấy ngay các cặp góc so le trong bằng nhau nên \(\Delta IOA=\Delta KOH\left(g-c-g\right)\Rightarrow OI=OK,OA=OH\)
Xét tam giác vuông IAH có IO là trung tuyến ứng với cạnh huyền nên OH = OA = OI.
Vậy nên OA = OI = OH = OK.
e)
1. Nếu tam giác ABC cân thì AH là đường cao đồng thời trung tuyến. Vậy thì AH = BH = CH.
Xét tam giác cân BHA có HI là đường cao nên đồng thời là đường trung tuyến. Vậy nên I là trung điểm AB.
Hoàn toàn tương tự ta có K là trung điểm AC.
2. Tam giác ABC vuông cân tại A nên \(\widehat{ACB}=45^o\)
IA = AB/2; AK = AC/2 mà AB = AC nên AI = AK.
Vậy thì tam giác IAK cũng vuông cân tại A.
Vậy nên \(\widehat{AKI}=45^o\)
Từ đó ta có \(\widehat{AKI}=\widehat{ACB}=45^o\)
Chúng lại ở vị trí đồng vị nên suy ra IK // BC.
f) Ta có AM = MC nên \(\widehat{MAC}=\widehat{MCA}\)
Lại có \(\widehat{MCA}=\widehat{AHK}\) (Cùng phụ với góc \(\widehat{KHC}\) )
Suy ra \(\widehat{MAC}=\widehat{AHK}\)
Lại có \(\widehat{OKA}=\widehat{OHA}\)
Vậy nên \(\widehat{MAK}+\widehat{OKA}=\widehat{AHK}+\widehat{IHA}=90^o\)
Gọi J là giao điểm của AM và IK thì \(\widehat{AJK}=90^o\) hay \(KI\perp AM\)
+ Vì O là giao điểm của ba đường phân giác trong tam giác ABC nên O là tâm của đường tròn nội tiếp tam giác ABC nên đáp án A sai.
+ Tam giác ABC vuông tại A có F là trung điểm của BC nên AF là đường trung tuyến ứng với cạnh huyền
Do đó: AF = 1 2 BC (trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
Suy ra AF = FC = FB
Nên F cách đều ba đỉnh A, B, C
Do đó F là tâm đường tròn ngoại tiếp tam giác ABC.
+ Vì D ≠ E ≠ F và chỉ có một đường tròn ngoại tiếp tam giác ABC nên đáp án B, C sai và D đúng.
Chọn đáp án D