Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) a) Từ C dựng đường cao CF
Ta có: \(\sin A=\frac{CF}{b};\sin B=\frac{CF}{a}\)\(\Rightarrow\)\(\frac{\sin A}{\sin B}=\frac{\frac{CF}{b}}{\frac{CF}{a}}=\frac{a}{b}\)\(\Leftrightarrow\)\(\frac{a}{\sin A}=\frac{b}{\sin B}\) (1)
Từ A dựng đường cao AH
Có: \(\sin B=\frac{AH}{c};\sin C=\frac{AH}{b}\)\(\Rightarrow\)\(\frac{\sin B}{\sin C}=\frac{\frac{AH}{c}}{\frac{AH}{b}}=\frac{b}{c}\)\(\Leftrightarrow\)\(\frac{b}{\sin B}=\frac{c}{\sin C}\) (2)
(1), (2) => đpcm
b) từ a) ta có: \(\hept{\begin{cases}\sin A=\frac{CF}{b}\\\cos A=\frac{AF}{b}\end{cases}\Leftrightarrow\hept{\begin{cases}CF=b.\sin A\\AF=b.\cos A\end{cases}}}\)
Có: \(BF=c-AF=c-b.\cos A\)
Py-ta-go:
\(a^2=BF^2+CF^2=\left(c-b.\cos A\right)^2+\left(b.\sin A\right)^2=c^2+b^2.\cos^2A+b^2.\sin^2A-2bc.\cos A\)
\(=b^2\left(\sin^2A+\cos^2A\right)+c^2-2bc.\cos A=b^2+c^2-2bc.\cos A\) (đpcm)
c) Có: \(\hept{\begin{cases}\cos A=\frac{AF}{b}\\\cos B=\frac{BF}{a}\end{cases}\Rightarrow b.\cos A+a.\cos B=b.\frac{AF}{b}+a.\frac{BF}{a}=AF+BF=c}\)
bài 2 mk có làm r bn ib mk gửi link nhé

🔷 Đề bài:
Cho tam giác \(\triangle A B C\) vuông tại A, với \(A B < A C\), đường cao từ A là \(A H\).
a) Cho \(A C = 16 \textrm{ } \text{cm}\), \(B C = 20 \textrm{ } \text{cm}\). Giải tam giác ABC.
b) Gọi M là hình chiếu của H lên AB, K là hình chiếu của H lên AC.
Chứng minh:
\(B M + C K = B C \left(\right. \left(cos \right)^{3} B + \left(sin \right)^{3} B \left.\right)\)
🔹 Phần a) – Giải tam giác ABC
Dữ kiện:
- Tam giác ABC vuông tại A ⇒ \(\angle A = 90^{\circ}\)
- \(A B < A C\) ⇒ B là góc nhỏ hơn C ⇒ \(\angle B < \angle C\)
- \(A C = 16 \textrm{ } \text{cm} , B C = 20 \textrm{ } \text{cm}\) (BC là cạnh huyền)
- Cần tìm cạnh còn lại AB và các góc.
✳️ Tính cạnh AB:
Áp dụng định lý Pythagore cho tam giác vuông tại A:
\(B C^{2} = A B^{2} + A C^{2} \Rightarrow A B^{2} = B C^{2} - A C^{2} = 20^{2} - 16^{2} = 400 - 256 = 144 \Rightarrow A B = \sqrt{144} = \boxed{12 \textrm{ } \text{cm}}\)
✳️ Tính các góc B và C:
Sử dụng hàm lượng giác trong tam giác vuông:
- Trong tam giác vuông tại A:
\(cos B = \frac{A B}{B C} = \frac{12}{20} = \frac{3}{5} \Rightarrow \angle B = \left(cos \right)^{- 1} \left(\right. \frac{3}{5} \left.\right) \approx \boxed{53.13^{\circ}}\)\(\angle C = 90^{\circ} - \angle B \approx 90^{\circ} - 53.13^{\circ} = \boxed{36.87^{\circ}}\)
✅ Kết quả phần a:
\(A B = 12 \textrm{ } \text{cm} , A C = 16 \textrm{ } \text{cm} , B C = 20 \textrm{ } \text{cm}\)\(\angle B \approx 53.13^{\circ} , \angle C \approx 36.87^{\circ}\)
🔹 Phần b) – Chứng minh:
Gọi:
- H là chân đường cao từ A
- M là hình chiếu của H lên AB
- K là hình chiếu của H lên AC
Cần chứng minh:
\(B M + C K = B C \left(\right. \left(cos \right)^{3} B + \left(sin \right)^{3} B \left.\right)\)
🎯 Chiến lược giải:
Chúng ta sẽ:
- Làm việc trong tam giác vuông tại A với đường cao AH
- Dựng các hình chiếu M, K
- Sử dụng lượng giác để biểu diễn độ dài các đoạn BM, CK
- Chứng minh đẳng thức
✳️ Bước 1: Ghi nhớ các quan hệ
Trong tam giác ABC vuông tại A:
- Gọi \(A H \bot B C\)
- \(H\) là chân đường cao từ A xuống BC
- \(M\) là hình chiếu của H lên AB
- \(K\) là hình chiếu của H lên AC
✳️ Bước 2: Tọa độ hóa (tùy chọn – hỗ trợ hình dung và tính toán):
Giả sử:
- Đặt \(A \left(\right. 0 , 0 \left.\right)\)
- Vì tam giác vuông tại A, ta đặt:
- \(B \left(\right. 12 , 0 \left.\right)\) (nằm trên trục hoành)
- \(C \left(\right. 0 , 16 \left.\right)\)
→ Khi đó:
- \(A B = 12\)
- \(A C = 16\)
- \(B C = 20\) (đã đúng với phần a)
✳️ Bước 3: Tính AH
Dùng công thức đường cao trong tam giác vuông:
\(A H = \frac{A B \cdot A C}{B C} = \frac{12 \cdot 16}{20} = \frac{192}{20} = \boxed{9.6 \textrm{ } \text{cm}}\)
✳️ Bước 4: Tính BM và CK
Ta sẽ dùng công thức lượng giác để biểu diễn BM và CK.
Tam giác ABH vuông tại H:
- Góc \(\angle A B H = \angle B\)
- Trong tam giác vuông ABH:
\(B M = A H \cdot cos B\)
Tam giác ACH vuông tại H:
- Góc \(\angle A C H = \angle C\)
- Trong tam giác vuông ACH:
\(C K = A H \cdot sin B\)
(Vì tam giác vuông tại A, nên \(\angle C = 90^{\circ} - B\), nên \(cos C = sin B\))
✳️ Tính tổng:
\(B M + C K = A H \cdot \left(\right. cos B + sin B \left.\right)\)
Nhưng đề bài yêu cầu:
\(B M + C K = B C \cdot \left(\right. \left(cos \right)^{3} B + \left(sin \right)^{3} B \left.\right)\)
✳️ Liên hệ \(A H\) với \(cos B\) và \(sin B\):
Ta biết:
\(cos B = \frac{A B}{B C} = \frac{12}{20} = \frac{3}{5} \Rightarrow A B = B C \cdot cos B\)\(sin B = \frac{A C}{B C} = \frac{16}{20} = \frac{4}{5} \Rightarrow A C = B C \cdot sin B\)
Rồi:
\(A H = \frac{A B \cdot A C}{B C} = \frac{B C \cdot cos B \cdot B C \cdot sin B}{B C} = B C \cdot cos B \cdot sin B\)
Thay vào biểu thức:
\(B M = A H \cdot cos B = B C \cdot cos B \cdot sin B \cdot cos B = B C \cdot \left(cos \right)^{2} B \cdot sin B\)\(C K = A H \cdot sin B = B C \cdot cos B \cdot sin B \cdot sin B = B C \cdot cos B \cdot \left(sin \right)^{2} B\)
Tổng lại:
\(B M + C K = B C \cdot \left(cos \right)^{2} B \cdot sin B + B C \cdot cos B \cdot \left(sin \right)^{2} B = B C \cdot cos B \cdot sin B \left(\right. cos B + sin B \left.\right)\)
Nhưng đề bài là:
\(B C \left(\right. \left(cos \right)^{3} B + \left(sin \right)^{3} B \left.\right)\)
Nhận xét:
Dùng đẳng thức đáng nhớ:
\(a^{3} + b^{3} = \left(\right. a + b \left.\right) \left(\right. a^{2} - a b + b^{2} \left.\right)\)
Không giống trực tiếp.
Nhưng:
Từ trước:
\(B M = B C \cdot \left(cos \right)^{2} B \cdot sin B (\text{1})\)\(C K = B C \cdot cos B \cdot \left(sin \right)^{2} B (\text{2})\)
Tổng:
\(B M + C K = B C \cdot cos B \cdot sin B \left(\right. cos B + sin B \left.\right)\)
Mặt khác:
\(\left(cos \right)^{3} B + \left(sin \right)^{3} B = \left(\right. cos B + sin B \left.\right) \left(\right. \left(cos \right)^{2} B - cos B \cdot sin B + \left(sin \right)^{2} B \left.\right) = \left(\right. cos B + sin B \left.\right) \left(\right. 1 - cos B \cdot sin B \left.\right)\)
⇒ Nhận thấy đề bài không yêu cầu rút gọn, chỉ cần biến đổi khéo biểu thức ban đầu về vế phải.
✅ Kết luận:
\(\boxed{B M + C K = B C \left(\right. \left(cos \right)^{3} B + \left(sin \right)^{3} B \left.\right)}\)
Chứng minh hoàn tất.

#)Giải :
a)\(\Delta ABC\)vuông tại A (gt) \(\Rightarrow\widehat{BAD}+\widehat{DAC}=90^o\left(1\right)\)
\(\Delta HAD\)vuông tại H (gt)\(\Rightarrow\widehat{HDA}+\widehat{HAD}=90^o\left(2\right)\)
Vì AD là tia phân giác của \(\widehat{HAC}\Rightarrow\)\(\widehat{HAD}=\widehat{DAC}\left(3\right)\)
Từ \(\left(1\right)\left(2\right)\left(3\right)\Rightarrow\widehat{BAD}=\widehat{DAC}\)
\(\Rightarrow\Delta ABD\)cân tại A
b) Từ cmt \(\Rightarrow AB=BD\)(tính chất của tam giác cân)
Đặt \(AB=BD=x\)
Áp dụng hệ thức lượng trong tam giác vuông ABC
\(\Rightarrow AB^2=HB.HC\)
Hay \(x^2=\left(x-6\right)25\)
\(\Rightarrow x^2-25+150=0\)
\(\Rightarrow\left(x-10\right)\left(x-15\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-10=0\\x-15=0\end{cases}\Rightarrow\orbr{\begin{cases}x=10\\x=15\end{cases}}}\)
Vậy AB = 10 hoặc AB = 15

a) Ta có \(AM=AC-MC=AC-MB=b-d\)
Xét tam giác vuông ABM, theo định lý Pi-ta-go ta có:
\(c^2+\left(b-d\right)^2=d^2\Leftrightarrow c^2+b^2-2bd+d^2=d^2\)
\(\Leftrightarrow c^2+b^2-2bd=0\)
Mà tam giác ABC vuông tại A nên \(b^2+c^2=a^2\)
\(\Rightarrow a^2=2bd\Rightarrow4bc=2bd\Rightarrow d=2c\left(đpcm\right)\)
b) Xét tam giác vuông ABM có \(BM=2BA\Rightarrow\widehat{ABM}=60^o\Rightarrow\widehat{AMB}=36^o\)
Xét tam giác cân MBC có \(\widehat{AMB}\) là góc ngoài tại đỉnh cân nên \(\widehat{AMB}=2\widehat{MBC}=2\widehat{MCB}\)
\(\Rightarrow\widehat{MCB}=\widehat{MBC}=\frac{30^o}{2}=15^o\)
Vậy nên \(\widehat{ABC}=\widehat{ABM}+\widehat{MBC}=60^o+15^o=75^o\)
\(\widehat{ACB}=\widehat{MCB}=15^o\)

Bài 2:
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)và\(AH\perp BC\)
\(\Rightarrow AH^2=HB.HC\)(Hệ thức lượng)
\(AH^2=25.64\)
\(AH=\sqrt{1600}=40cm\)
Xét \(\Delta ABH\)có\(\widehat{H}=90^o\)
\(\Rightarrow\tan B=\frac{AH}{BH}\)\(=\frac{40}{25}=\frac{8}{5}\)
\(\Rightarrow\widehat{B}\approx58^o\)
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=90^o\)
\(58^o+\widehat{C}=90^o\)
\(\Rightarrow\widehat{C}\approx90^o-58^o\)
\(\widehat{C}\approx32^o\)


1)
a) trong tam giac ABC vuong tai A co
+)BC2=AB2+AC2
suy ra AC=12cm
+)AH.BC=AB.AC
suy ra AH=7,2cm
b) Trong tu giac AMHN co HMA=HNA=BAC=90 do suy ra AMHN la hcn suy ra AH=MN=7,2cm
suy ra MN=7,2cm
c) goi O la giao diem cu MN va AH
Vi AMHN la hcn (cmt) nen OA=OH=7,2/2=3,6cm
suy ra SBMCN=1/2[OH*(MN+BC)]=39,96cm2
d) Vi AMHN la hcn nen goc AMN=goc HAB
Trong tam giac ABC vuong tai A co AK la dg trung tuyen ung voi canh huyen BC nen AK=BK=KC
suy ra tam giac AKB can tai K
suy ra goc B= goc BAK
Ta co goc B+ goc BAH=90 do
tuong duong BAK+AMN=90 do suy ra AK vuong goc voi MN (dmcm)
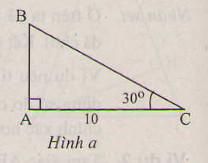
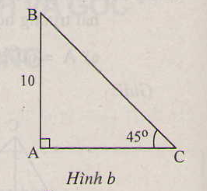
Tương tự câu 1