Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c) Gọi O là giao điểm của BE và AF
Xét tam giác AHC có: M là TĐ của HC(gt) , E là TĐ của AC (gt)
\(\Rightarrow ME\)là đường trung bình của tam giác AHC
\(\Rightarrow ME//AH\left(tc\right)\)
Mà \(AH\perp BC\)
\(\Rightarrow ME\perp BC\)
\(\Rightarrow\widehat{BME}=90^0\)
Vì ABFE là hcn (cmt)
\(\Rightarrow BE\)cắt AF tại TĐ mỗi đường (tc) mà O là giao điểm của BE và AF(c.vẽ)
\(\Rightarrow O\)là TĐ của BE và AF
Xét tam giác \(BME\)vuông tại M có đường trung tuyến OM ứng với cạnh huyền BE
\(\Rightarrow OM=\frac{1}{2}BE\left(tc\right)\)
Mà \(BE=AF\)(tc hcn)
\(\Rightarrow OM=\frac{1}{2}AF\)
Xét tam giác AMF có trung tuyến OM ứng với cạnh AF và \(OM=\frac{1}{2}AF\left(cmt\right)\)
\(\Rightarrow\Delta AMF\)vuông tại M
\(\Rightarrow\widehat{FMA}=90^0\)
\(\Rightarrow AM\perp FM\)

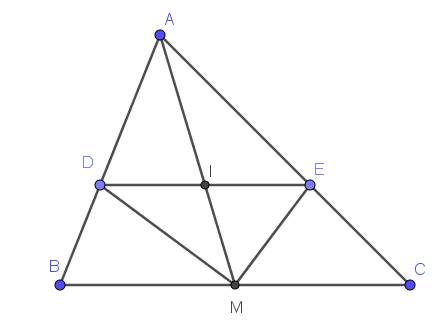
Lời giải:
a. Áp dụng tính chất tia phân giác đối với tam giác $AMB, AMC$ thì:
$\frac{AD}{DB}=\frac{AM}{MB}$
$\frac{AE}{EC}=\frac{AM}{MC}$
Mà $MB=MC$ (do $M$ là trung điểm $BC$)
$\Rightarrow \frac{AD}{DB}=\frac{AE}{EC}$
$\Rightarrow DE\parallel BC$ (theo định lý Talet đảo)
b.
Tam giác $ABM$ có $DI\parallel BM$ (do $DE\parallel BC$) nên áp dụng định lý Talet:
$\frac{DI}{BM}=\frac{AI}{AM}$
Tam giác $ACM$ có $IE\parallel CM$ (do $DE\parallel BC$) nên áp dụng định lý Talet:
$\frac{IE}{MC}=\frac{AI}{AM}$
$\Rightarrow \frac{DI}{BM}=\frac{IE}{MC}$
Mà $BM=CM$ nên $DI=IE$
$\Rightarrow I$ là trung điểm $DE$>