Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

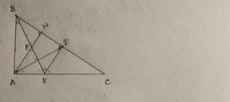
b) Ta có: KI\(\perp\)BC(gt)
AH\(\perp\)BC(gt)
Do đó: KI//AH(Định lí 1 từ vuông góc tới song song)
Suy ra: \(\widehat{HAI}=\widehat{KIA}\)(hai góc so le trong)(1)
Ta có: ΔABK=ΔIBK(cmt)
nên KA=KI(hai cạnh tương ứng)
Xét ΔKAI có KA=KI(cmt)
nên ΔKAI cân tại K(Định nghĩa tam giác cân)
Suy ra: \(\widehat{KAI}=\widehat{KIA}\)(hai góc ở đáy)(2)
Từ (1) và (2) suy ra \(\widehat{HAI}=\widehat{KAI}\)
\(\Leftrightarrow\widehat{HAI}=\widehat{CAI}\)
Suy ra: AI là tia phân giác của \(\widehat{HAC}\)(Đpcm)
a) Xét ΔABK vuông tại A và ΔIBK vuông tại I có
BK chung
\(\widehat{ABK}=\widehat{IBK}\)(BK là tia phân giác của \(\widehat{ABI}\))
Do đó: ΔABK=ΔIBK(Cạnh huyền-góc nhọn)

a: Xét ΔABK và ΔIBK có
BA=BI
\(\widehat{ABK}=\widehat{IBK}\)
BK chung
Do đó: ΔABK=ΔIBK
Suy ra: \(\widehat{BAK}=\widehat{BIK}=90^0\)
hay KI⊥BC
b: Ta có: \(\widehat{HAI}+\widehat{BIA}=90^0\)
\(\widehat{CAI}+\widehat{BAI}=90^0\)
mà \(\widehat{BIA}=\widehat{BAI}\)
nên \(\widehat{HAI}=\widehat{CAI}\)
hay AI là tia phân giác của góc HAC
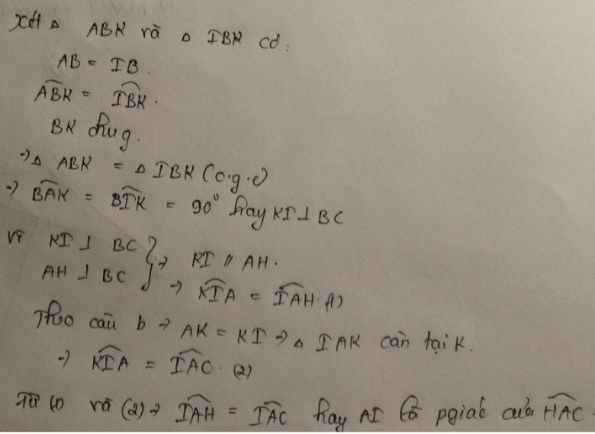
giúp mình ạ mình con 20p thôi ạ
bn tham khảo tại đây;
https://olm.vn/hoi-dap/detail/256733768368.html