Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
4 bài toàn là hình, lại khó, dài , mk nghĩ chắc ko ai tl giúp bn đâu, xl nha, ngay mk mới lp 6 cx chưa thể giải đc vì đã lp 7 đâu. ah hay là bn gửi tg bài 1 cho các bn ấy giải từ từ, cứ 1 đốg thì ai giải giúp bn đc. sorry nha
*In đậm: quan trọng.
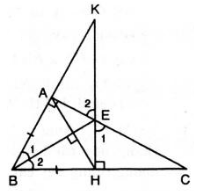
Xét ΔABE và ΔHBE có:
\(\widehat{BAE}=\widehat{BHE}=90\) (gt)
BE:cạnh chung
\(\widehat{ABE}=\widehat{HBE}\left(gt\right)\)
=> ΔABE =ΔHBE(cạnh huyền-góc nhọn)
b) Vì ΔABE=ΔHBE(cmt)
=> AB=BH ; AE=EH
=> B,E \(\in\) đường trung trực của đoạn thẳng AH
=>BE là đường trung trực của đoạn thẳng AH
c) Xét ΔAEK và ΔHEC có:
\(\widehat{KAE}=\widehat{CHE}=90\left(gt\right)\)
AE=EH(cmt)
\(\widehat{AEK}=\widehat{HEC}\)
=>ΔAEK=ΔHEC(g.c.g)
=>EK=EC
d) Xét ΔEHC vuông tại H(gt)
=> HE<EC
Mà: HE=AE(cmt)
=>AE<EC
d) Xét ΔHKC có:
KH,CA là hai đường cao
=> E là trực tâm của ΔBKC
=>BE là đường cao
=> AE vuông góc KC
a)
xét 2 tam giác vuông ABE và HBE có:
BE(chung)
góc ABE= góc CBE(gt)
=> ΔABE=ΔHBE(CH-GN)
b)
gọi giao của BE và AH là F
xét ΔABF và ΔHBF có:
AB=HB(theo câu a, ΔABE=ΔHBE)
BF(chung)
góc ABE=góc HBE(gt)
=> ΔABF=ΔHBF(c.g.c)
=>\(\begin{cases}FA=FH\\\widehat{AFB}=\widehat{BFH}=180^o:2=90^o\end{cases}\)
=> BE là đường trung trực của AH
c)
xét ΔAEK và ΔHEC có:
EA=EH(theo câu a, ΔABE=ΔHBE)
góc KAE=góc EHC=90º(gt)
góc AEK=góc CEH(2 góc đối đỉnh)
=>ΔAEK=ΔHEC(g.c.g)
=>EK=EC
d)
ta có ΔAEK vuông tại A
=> EK>AE
mà EK=EC(theo câu c)
=> AE<EC
e)
theo câu a, ta có: ΔABE=ΔHBE(CH-GN)
=>AB=HB
theo câu c, ta có: ΔAEK=ΔHEC(g.c.g)
=> AK=HC
ta có: KB=KA+AB
CB=CH+HB
=>KB=CB
=>ΔKBC cân tại B
ta có:ΔKCB cân tại B có BE là đường phân giác
=>BE đồng thời là đường cao của ΔKBC
=>BE_|_KC
f)
áp dụng định lí py-ta-go ta có;
\(AC^2=BC^2-AB^2=5^2-3^2=25-9=16\)
\(AC=\sqrt{16}=4\left(cm\right)\)
theo câu e; ta có ΔKBC cân tại B
=> BC=BK=5cm
AK=BC-AB=5cm-3cm=2cm
áp dụng định lí py-ta-go ta có:
\(KC^2=AK^2+AC^2=4^2+2^2=16+4=20\)
\(KC=\sqrt{20}\left(cm\right)\)
a) Tam giác ABE và tam giác HBE có góc A = góc H = 90độ, góc ABE = góc HBE, cạnh huyền BE chung nên hai tam giác đó bằng nhau.
b) từ hai tam giác trên bằng nhau suy ra BA = BH, EA = EH suy ra B và E cùng thuộc đường trung trực của AH suy ra BE là đường trung trực của AH.
c) c/m hai tam giác vuông AKE và HCE bằng nhau theo trường hợp góc cạnh góc. suy ra EK = EC.
d) tam giác AKE vuông tại A nên AE<EK mà EK = EC nên AE < EC.
a. Áp dụng đ/l Pytago có
\(AC^2=BC^2-AB^2=100-36\)
=> AC = 8 (cm)
b/ Xét t/g ABE vg tại A và t/g HBE cg tại H có
BE chung
\(\widehat{ABE}=\widehat{CBE}\)
=> t/g ABE = t/g HBE
=> AB = HB ; AE = HE (*)
Xét t/g HEC vg tại H => EC > HE
=> AE < EC
c/ Xét t.g BCK có
KH vg góc BC
CA vg góc BK
CA cắt HK tại E
=> E là trực tâm t/g BCK
=> BE ⊥ CK (1)
(*) => BE là đường trung trực của AH
=> BE ⊥ AH (2)
(1) ; (2)
=> CK // AH
d/ Xét t.g BAH có AB = AH ; \(\widehat{ABH}=60^o\)
=> t/g BAH đều
cảm ơn ạ!