Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
ΔEHC vuông tại H có EH < EC (cạnh huyền là lớn nhất trong tam giác vuông)
mà EH = AE (câu b) nên AE < EC.
Xét ΔAEK vuông tại A và ΔHEC vuông tại H có:
AE = EH (chứng minh trên)
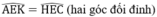
⇒ ΔAEK = ΔHEC (cạnh góc vuông – góc nhọn kề)
⇒ EK = EC (hai cạnh tương ứng)
Xét ΔABE vuông tại A và ΔHBE vuông tại H có :
BE chung
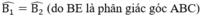
⇒ ΔABE = ΔHBE (cạnh huyền – góc nhọn)
Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)
Do đó: ΔBAE=ΔBHE
Suy ra: BA=BH và EA=EH
Xét ΔEAK vuông tại A và ΔEHC vuông tại H có
EA=EH
\(\widehat{AEK}=\widehat{HEC}\)
Do đó: ΔEAK=ΔEHC
Suy ra: AK=HC
Ta có: BA+AK=BK
BH+HC=BC
mà BA=BH
và AK=HC
nên BK=BC
hay ΔBKC cân tại B
ΔABE = Δ HBE
⇒ BA = BH, EA = EH (các cặp cạnh tương ứng)
⇒ E, B cùng thuộc trung trực của AH
nên đường thẳng EB là trung trực của AH.
a, xét tam giác ABE và tam giác HBE có : BE chung
góc BAE = góc BHE = 90 do ...
góc ABE = góc HBE do BE là phân giác ...
=> tam giác ABE = tam giác HBE (ch - gn)
=> AE = EH
b, xét 2 tam giác vuông EAK và EHC có:
EA=EH(theo câu a)
ˆAEKAEK^=ˆHECHEC^(vì đối đỉnh)
=> t.giác EAK=t.giác EHC(cạnh góc vuông-góc nhọn)
=> EK=EC(2 cạnh tương ứng)
c, ta thấy E là trực tâm của tam giác CKB
=> BE⊥⊥CK
tham khảo
a, xét tam giác ABE và tam giác HBE có : BE chung
góc BAE = góc BHE = 90 do ...
góc ABE = góc HBE do BE là phân giác ...
=> tam giác ABE = tam giác HBE (ch - gn)
=> AE = EH
b, xét 2 tam giác vuông EAK và EHC có:
EA=EH(theo câu a)
ˆAEKAEK^=ˆHECHEC^(vì đối đỉnh)
=> t.giác EAK=t.giác EHC(cạnh góc vuông-góc nhọn)
=> EK=EC(2 cạnh tương ứng)
c, ta thấy E là trực tâm của tam giác CKB
=> BE⊥CK
a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
góc ABE=góc HBE
=>ΔBAE=ΔBHE
=>EA=EH
b: Xét ΔEAK vuông tại A và ΔEHC vuông tại H có
EA=EH
góc AEK=góc HEC
=>ΔEAK=ΔEHC
=>EK=EC
c: BK=BC
EK=EC
=>BE là trung trực của CK
=>BE vuông góc CK
a. Áp dụng đ/l Pytago có
\(AC^2=BC^2-AB^2=100-36\)
=> AC = 8 (cm)
b/ Xét t/g ABE vg tại A và t/g HBE cg tại H có
BE chung
\(\widehat{ABE}=\widehat{CBE}\)
=> t/g ABE = t/g HBE
=> AB = HB ; AE = HE (*)
Xét t/g HEC vg tại H => EC > HE
=> AE < EC
c/ Xét t.g BCK có
KH vg góc BC
CA vg góc BK
CA cắt HK tại E
=> E là trực tâm t/g BCK
=> BE ⊥ CK (1)
(*) => BE là đường trung trực của AH
=> BE ⊥ AH (2)
(1) ; (2)
=> CK // AH
d/ Xét t.g BAH có AB = AH ; \(\widehat{ABH}=60^o\)
=> t/g BAH đều
1. ΔABE = ΔHBE
Xét ΔABE và ΔHBE, ta có :
BE là cạnh chung.
=> ΔABE = ΔHBE
2. BE là đường trung trực của AH :
BA =BH và EA = EH (ΔABE = ΔHBE)
=> BE là đường trung trực của AH .
3. EK = EC
Xét ΔKAE và ΔCHE, ta có :
EA = EH (cmt)
=> ΔKAE và ΔCHE
=> EK = EC
4. EC > AC
Xét ΔKAE vuông tại A, ta có :
KE > AE (KE là cạnh huyền)
Mà : EK = EC (cmt)
=> EC > AC.
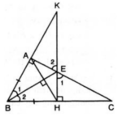
Bạn ơi, cái đề bạn ghi còn thiếu bạn chưa cho chứng minh rằng cái gì ? MIK VẼ CHO BẠN CÁI HÌNH NÈ. CÒN CHỨNG MINH BẠN GHI THIẾU