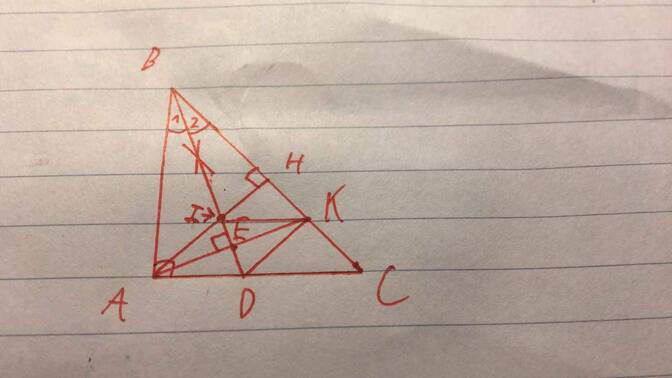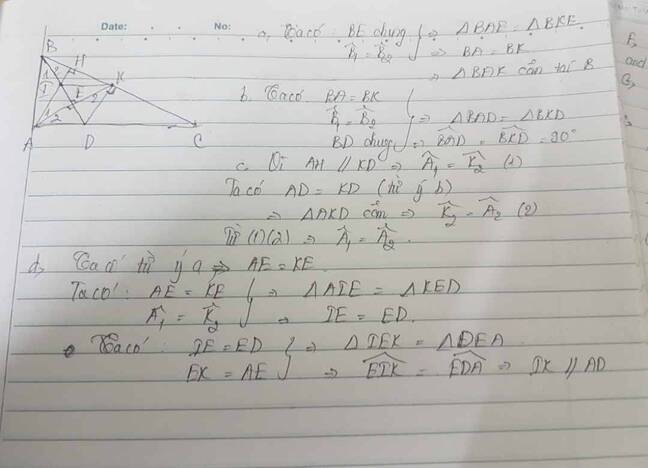Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) xét ABE vuông tại E và KBE vuông tại E
có góc ABE =KBE(gt)
BE chug
=> ABE=KBE ( ch -gn)
=> AB=KB( cạnh t/ư)
=> ABK cân tại B
b) xét ABD và KBD
có AB=KB
ABD=KBD
BD chung
=> ABD = KBD( cgc)
=> BAD = BKD
mà BAD = 90 độ
=> BKD =90 độ
hay DK vuông góc BC tại K

a) Xét tam giác vuông ABE và tam giác vuông KBE có
Cạnh BE chung
DBA=DBK hay EBA=EBA ( vì BD là phân giác của góc ABC)
=>\(\Delta ABE=\Delta KBE\) ( cạnh góc vuông- góc nhọn)
=>BA=BK
Vậy tam giác ABK cân tại B
b) Xét \(\Delta ABD\) và \(\Delta KBD\) có
AB=BK
ABD=KBD
Cạnh BD chung
=> \(\Delta ABD=\Delta KBD\left(c.g.c\right)\)
=> DKB=DAB=90 độ
Vậy \(DK⊥BC\)
c)d)
Xét \(\Delta ABI\) và \(\Delta KBI\) có
BA=BK
ABI=FBI
Cạnh BF chung
=> \(\Delta ABI=\Delta KBI\left(c.g.c\right)\)
=> IA=IK
Ta có DA=DK, IA=IK hay ID là đường trung trực của AK
=>AE=EK
Có \(DK⊥BC,AH⊥BC\) => DK//AH
=>DKE=EAI( 2 góc so le trong)
Xét tam giác vuông DKE và tam giác vuông EAI có
AE=EK
DKE=EAI
=> \(\Delta DKE=\Delta EAI\)(cạnh góc vuông- góc nhọn)
=>DK=AI
Mà DK=DA
=>AI=AD
Xét tam giác vuông DAE và tam giác vuông IAE có
DA=DI
Cạnh AE chung
=> \(\Delta DAE=\Delta IAE\)( cạnh huyền- cạnh góc vuông)
=>DAE=EAI hay góc CAK= góc KAH
Vậy AK là phân giác của HAC
Xét tam giác vuông IKE và tam giác vuông EAD có
AE=EK
KEI=AED( 2 góc đối đỉnh)
=>\(\Delta IKE=\Delta EAD\)( cạnh góc vuông- góc nhọn)
=>IKE=EAD
Mà IKE và EAD là 2 góc so le trong =>IK//AC

a) Có tam giác ABC vuông tại A
=>\(BC^2=AC^2+AB^2\) ( định lí Pitago)
=>\(BC^2=8^2+6^2=100\)
=> BC=10 (cm)
b) Xét tam giác vuông ABE và tam giác vuông KBE có
Cạnh BE chung
Góc DBA= góc DBK hay góc EBA= góc EBK ( vì BD là tia phân giác của góc ABC)
=> tam giác ABE= tam giác KBE( cạnh góc vuông- góc nhọn)
=> BA=BK ( 2 cạnh tương ứng)
Vạy tam giác ABK cân tại B
c) Nối D với K, ta có tam giác DKE vuông tại E
Theo câu b, ta có tam giác ABE= tam giác KBE
=> KE=EA( 2 cạnh tương ứng) và góc EAB=góc EKB (1)
Xét tam giác vuông DEA và tam giác vuông DEK có
Cạnh DE chung
EA=KE
=> tam giác DEA= tam giác DEK ( 2 cạnh góc vuông)
=> Góc DAE=góc DKE (2)
Từ (1) và (2) =>góc DKE+ góc EKB=góc DAE+ góc EAB= góc DAB=90 độ
=> Góc DKB= 90 độ
Vậy DK vuông góc với BC
d)
Có \(DK⊥BC,AH⊥BC\) =>DK//AB
=> góc DKE= góc EAH (1)
Có tam giác DEA=tam giác DEK
=> góc DAE= góc DKE (2)
Từ (1) và (2) => góc EAH= góc DAE hay góc CAK= góc KAH
Vậy AK là phân giác của góc HAC

ban tu ve hinh
a) +) tam giac ABE co : ABE+BAE+BEA=180( dinh li tong 3 goc cua 1 tam giac)
ABE+BAE+90=180
ABE+BAE =180-90=90(1)
+) tam giac EBK co : EBK+KEB+BKE=180(dinh li tong 3 goc cua 1 tam giac )
EBK+90+BKE=180
EBK+BKE=90(2)
Vi ABE=EBK(BD la phan giac cua ABC) nen tu (1) va (2) suy ra BAE=BKE
suy ra tam giac BAK can tai B
b)Vi tam giac ABK can tai B nen AB=BK
xet tam giac ABD va tam giac KBD CO :
BD chung
ABD=KBD ( BD la phan giac cua ABC)
AB=AK(cmt)
NEN tam giac ABD= tam giaac KBD (c-g-c) nen AB=BK( 2 canh tuong ung ) ;BAD=BKD(2 goc tuong ung ) ma BAD=90 NEN DKB=90
SUY RA DK vuong goc voi BC
CAC GOC KO CO KI HIEU MU GOC BAN TU THEM VAO

a: Xét ΔBAK có
BE là đường cao
BE là đường trung tuyến
Do đó: ΔBAK cân tại B
b: Xét ΔBAD và ΔBKD có
BA=BK
\(\widehat{ABD}=\widehat{KBD}\)
BD chung
Do đó: ΔBAD=ΔBKD
Suy ra: \(\widehat{BAD}=\widehat{BKD}=90^0\)

a. Xét Δ ABE và Δ KBE có:
^B1=^B2(BD là tia p/g)
^BEA=^KEB=90o
AE chung
=> ΔABE=ΔKBE(g.c.g)
=>AB=KB
=>ΔABK cân tại B
(xin lỗi mình ko biết phần b,c,d) ;-;
cho bạn cái hình nè :