Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

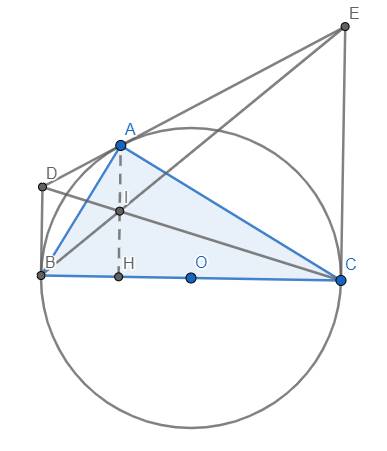
a) Theo tính chất của 2 tiếp tuyến cắt nhau \(\left\{{}\begin{matrix}AD=BD\\AE=CE\end{matrix}\right.\)
\(\Rightarrow\dfrac{AD}{AE}=\dfrac{BD}{CE}=\dfrac{ID}{IC}\)
\(\Rightarrow\) AI//CE.
Mà \(CE\perp BC\) nên \(AI\perp BC\)
Lại có \(AH\perp BC\) \(\Rightarrow\) A, I, H thẳng hàng (đpcm)
b) Theo định lý Thales, ta có \(\dfrac{AI}{CE}=\dfrac{DA}{DE}\) và \(\dfrac{IH}{CE}=\dfrac{BH}{BC}\)
Mặt khác, \(\dfrac{DA}{DE}=\dfrac{BH}{BC}\) (đl Thales trong hình thang)
\(\Rightarrow\dfrac{AI}{CE}=\dfrac{IH}{CE}\) \(\Rightarrow AI=IH\) (đpcm)
c) Ta có \(\dfrac{DB}{DE}=\dfrac{DA}{DE}=\dfrac{AI}{CE}\) \(\Rightarrow DB.CE=DE.AI\) (đpcm)

a: Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
Xét ΔABC có
BE là đường cao
CF là đường cao
BE cắt CF tại H
Do đó: AH⊥BC
hay AF⊥BC

b: Xét ΔAHB vuông tại H có HD là đường cao ứng với cạnh huyền AB
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
hay \(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Xét ΔADE vuông tại A và ΔACB vuông tại A có
\(\dfrac{AD}{AC}=\dfrac{AE}{AB}\)
Do đó: ΔADE\(\sim\)ΔACB
Suy ra: \(\widehat{ADE}=\widehat{ACB}\)

a: \(AH=\sqrt{2\cdot4}=2\sqrt{2}\left(cm\right)\)
\(AB=\sqrt{AH^2+HB^2}=2\sqrt{3}\left(cm\right)\)