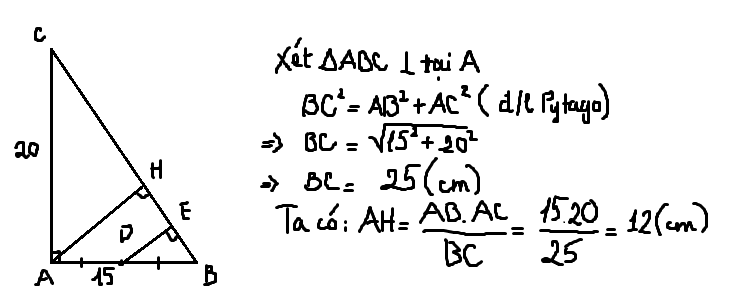Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:\(BC=\sqrt{AB^2+AC^2}=25\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{15\cdot20}{25}=12\left(cm\right)\)

Bài 26 : Bài giải
a. Do AB⊥AC,HE⊥AB,HF⊥ACAB⊥AC,HE⊥AB,HF⊥AC
⇒ˆEAF=ˆAEH=ˆAFH=90o⇒EAF^=AEH^=AFH^=90o
→◊AEHF→◊AEHF là hình chữ nhật
→AH=EF
Mấy câu khác chưa học !

a) Áp dụng định lý PYTAGO vào tam giác ABC có
BC^2=AB^2+AC^2
= 9^2+12^2=225
BC= 15
Sabc= 1/2.AB.AC = 54 mà Sabc = 1/2.AH.BC
=> 1/2.AH = Sabc: BC = 3.6=> AH =7,2

a: góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
góc MAC+góc AED=90 độ
=>góc MAC+góc AHD=90 độ
=>góc MAC+góc B=90 độ
=>góc MAC=góc MCA và góc MAB=góc MBA
=>MA=MB=MC
=>M là trung điểm của BC
b: \(BC=\sqrt{15^2+20^2}=25\left(cm\right)\)
AH=15*20/25=12cm
HB=15^2/25=9cm
HC=20^2/25=16(cm)
AD=12^2/15=144/15=9,6cm
AE=12^2/20=7,2cm
\(S_{ADE}=\dfrac{1}{2}\cdot7.2\cdot9.6=34.56\left(cm^2\right)\)