Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

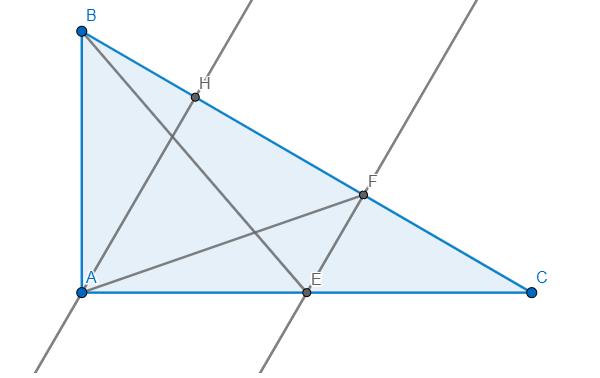
a) Xét \(\Delta CAH:\) ta có: E là trung điểm AC và \(EF\parallel AH(\bot BC)\)
\(\Rightarrow F\) là trung điểm CH \(\Rightarrow EF\) là đường trung bình \(\Rightarrow EF=\dfrac{1}{2}AH\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AH^2=BH.CH\)
Ta có: \(EF^2=\left(\dfrac{1}{2}AH\right)^2=\dfrac{1}{4}AH^2=\dfrac{1}{4}.BH.HC\)
b) Ta có: \(\angle BAE+\angle BFE=90+90=180\Rightarrow ABFE\) nội tiếp
\(\Rightarrow\angle FBE=\angle FAE\)
Xét \(\Delta CBE\) và \(\Delta CAF:\) Ta có: \(\left\{{}\begin{matrix}\angle CBE=\angle CAF\\\angle BCAchung\end{matrix}\right.\)
\(\Rightarrow\Delta CBE\sim\Delta CAF\left(g-g\right)\Rightarrow\dfrac{AF}{BE}=\dfrac{AC}{BC}=cosC\Rightarrow AF=cosC.BE\)

b: Xét ΔCFE vuông tại F và ΔCAB vuông tại A có
\(\widehat{C}\)chung
Do đó: ΔCFE\(\sim\)ΔCAB
Suy ra: \(\dfrac{CF}{CA}=\dfrac{CE}{CB}\)
\(\Leftrightarrow CF\cdot CB=CE\cdot CA\)
\(\Leftrightarrow CF\cdot CB=CA\cdot\dfrac{1}{2}AC\)
\(\Leftrightarrow AC^2=2\cdot CF\cdot CB\)
a: Xét ΔAHC có
E là trung điểm của AC
EF//AH
Do đó: F là trung điểm của CH
Xét ΔAHC có
E là trung điểm của AC
F là trung điểm của CH
Do đó: EF là đường trung bình của ΔAHC
Suy ra: \(EF=\dfrac{AH}{2}\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền CB
nên \(AH^2=HB\cdot HC\)
hay \(AH=\sqrt{HB\cdot HC}\left(2\right)\)
Từ (1) và (2) suy ra \(EF=\dfrac{\sqrt{HB\cdot HC}}{2}\)
hay \(EF^2=\dfrac{HB\cdot HC}{4}\)