Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: AC=8cm
b: \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{6\cdot8}{2}=24\left(cm^2\right)\)
c: AH=4,8cm
bn ơi câu a bn giải thích ra luôn giùm mik ik
câu b,c nx

a,
xét tam giác BAC và tam giác BHA có
góc B chung
góc BAC=góc BHA (=90 độ)
=>tam giác BAC đông dạng với tam giác BHA
ta có \(\dfrac{AB}{BH}=\dfrac{BC}{BA}\)=>\(AB^2=BH.BC\)
b,
Xét Tam giác ABC
=>\(\dfrac{AB}{AH}=\dfrac{BC}{AC}\)=>AB.AC=AH.BC
c,
áp dụng định lý py-ta-go vào tam giác ABC vuông tại A
\(AC^2=BC^2-BA^2\)
=>AC=8
Xét tam giác ABC
\(\dfrac{AC}{CH}=\dfrac{AB}{BH}=>\dfrac{8}{CH}=\dfrac{6}{10-CH}\)
=>8(10-CH)=6CH
=>80-8CH=6CH
=>CH sấp sỉ 5cm
áp dụng định lý py-ta-go vào tam giác HBA vuuong tại H
\(AH^2=AB^2-BH^2\)
=>AH=3,31662479

Bài 1:
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=5^2-3^2=16\)
hay AC=4cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{3^2}{5}=1.8\left(cm\right)\\CH=\dfrac{4^2}{5}=3.2\left(cm\right)\end{matrix}\right.\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot5=3\cdot4=12\)
hay AH=2,4cm
Bài 2:
Ta có: BC=HB+HC
nên BC=3,6+6,4
hay BC=10cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB^2=3.6\cdot10=36\\AC^2=6.4\cdot10=64\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=6\left(cm\right)\\AC=8\left(cm\right)\end{matrix}\right.\)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow AH^2=6^2-3.6^2=23.04\)
hay AH=4,8cm

a/ \(BD\) là đường phân giác \(\widehat{BAC}\)
\(\to\dfrac{DA}{DC}=\dfrac{BA}{BC}\) hay \(\dfrac{DA}{DC}=\dfrac{6}{10}=\dfrac{3}{5}\)
\(\to\dfrac{DA}{3}=\dfrac{DC}{5}=\dfrac{DA+DC}{3+5}=\dfrac{AC}{8}=\dfrac{8}{8}=1\)
\(\to\begin{cases}DA=3\\DC=5\end{cases}\)
b/ \(S_{\Delta ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.AH.BC\)
\(\to AB.AC=AH.BC\)
\(\to \dfrac{AB.AC}{BC}=AH=\dfrac{6.8}{10}=3,2(cm)\)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)
Vậy: AH=4,8cm

Áp dụng định lý Py – ta – go vào tam giác ABC vuông tại A ta có:
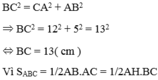
⇒ AH.BC = AB.AC
Hay 12.5 = AH.13 ⇒ AH = 60/13 ( cm )
Từ câu a ta có: Δ BHA ∼ Δ BAC ⇒ BH/BA = BA/BC hay BH/5 = 5/13 ⇔ BH = 25/13( cm )
Do đó: CH = BC - BH = 13 - 25/13 = 144/13( cm )

Lời giải:
1) Xét tam giác $BHA$ và $BAC$ có:
$\widehat{B}$ chung
$\widehat{BHA}=\widehat{BAC}=90^0$
$\Rightarrow \triangle BHA\sim \triangle BAC$ (g.g)
$\Rightarrow \frac{BH}{BA}=\frac{BA}{BC}$
$\Rightarrow BH=\frac{BA^2}{BC}=\frac{6^2}{8}=4,5$ (cm)
$CH=BC-BH=8-4,5=3,5$ (cm)
Áp dụng định lý Pitago:
$AC=\sqrt{BC^2-AB^2}=\sqrt{8^2-6^2}=2\sqrt{7}$ (cm)
$AH=\frac{AB.AC}{BC}=\frac{6.2\sqrt{7}}{8}=\frac{3\sqrt{7}}{2}$ (cm)
2. 3. Những phần này bạn làm tương tự như phần 1.

a: Xet ΔABC vuông tại A co AH là đường cao
nên AH^2=HB*HC
b: BC=3,6+6,4=10cm
\(AH=\sqrt{3.6\cdot6.4}=4.8\left(cm\right)\)
\(AB=\sqrt{3.6\cdot10}=6\left(cm\right)\)
=>AC=8cm
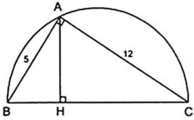
Có BC=CH+BH
=>BH=3,6cm
xét tam giác BHA và tam giác BAC
(bn tự c/m nha )
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BC}\)
=> AB2=BH.BC
bn thay số và tính vào nha