Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có \(\widehat{BNC}=\widehat{BMC}=90độ\)(gt)
Nên tứ giác BNMC nội tiếp (2 đỉnh N,M cùng BC với 2 góc bằng nhau)
(Câu sau không rõ. Cái gì là tâm đường tròn nội tiếp ΔMNH?)
b) Xét ΔAMN và ΔABC có:
\(\widehat{BAC}\)chung
\(\widehat{AMN}=\widehat{ABC}\)(tứ giác BNMC nội tiếp)
Do đó ΔAMN ~ ΔABC
Nên\(\frac{AM}{AB}=\frac{AN}{AC}\)
hay AM.AC=AN.AB
Ta có \(\widehat{ANH}=\widehat{AMH}=90độ\left(gt\right)\)
Nên \(\widehat{ANH}+\widehat{AMH}=180độ\)
Suy ra tứ giác ANHM nội tiếp
Do đó \(\widehat{NAM}+\widehat{NHM}=180độ\)
Mà \(\widehat{NHM}=\widehat{BHC}\)(đối đỉnh)
\(\widehat{BHC}=\widehat{BLC}\)(tính chất đối xứng trục)
Nên \(\widehat{NAM}+\widehat{BLC}=180độ\)
Suy ra tứ giác ABLC nội tiếp đường tròn (O) (tổng 2 góc đối bằng 180độ)
c) (Câu này hình như bạn ghi sai đề rồi, nếu I là giao điểm AH với AN thì I sẽ trùng với A. Nên mình nghĩ I là giao điểm MN với AH)
Ta có \(\widehat{HDC}=\widehat{HMC}=90độ\left(gt\right)\)
Nên \(\widehat{HDC+}\widehat{HMC}=180độ\)
Do đó tứ giác HMCD nội tiếp
Suy ra \(\widehat{HMD}=\widehat{HCD}\)
Mà \(\widehat{HCD}=\widehat{HMN}\)(tứ giác BMNC nội tiếp)
Nên \(\widehat{HMD}=\widehat{HMN}\)
Vậy MH là phân giác \(\widehat{NMD}\)
Mà MH vuông góc AM (gt)
Nên AM là phân giác ngoài
Do đó \(\frac{IH}{ID}=\frac{AH}{AD}\)
hay IH.AD=AH.ID
a.Ta có :
ˆAFH=ˆADB=90o→ΔAFH∼ΔADB(g.g)
→AFAD=AHAB→AF.AB=AH.AD
Tương tự AH.AD=AE.AC→AF.AB=AE.AC
b.Ta có :
ˆHFA=ˆHEA=ˆHFB=ˆHDB=90o
→AEHF,AEDB,FHDB nội tiếp
→ˆHFE=ˆFAE=ˆHBD=ˆHFD
→FH là phân giác ˆDFE
Mà FA⊥FH→FA là phân giác góc ngoài tại đỉnh F của ΔDEF
→HIHD=FIFD=AIAD
→IH.AD=AI.DH

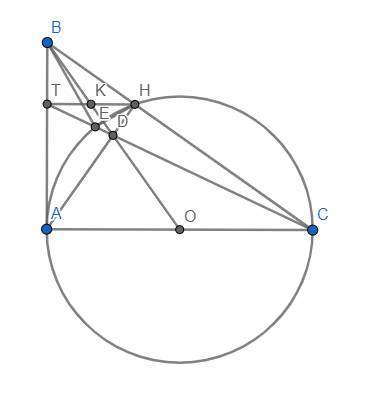
Gọi T là giao điểm của CD và AB. Khi đó xét tứ giác ACHT, ta có:
O (trung điểm AC), D (giao điểm của 2 đường chéo) và B (giao điểm của 2 đường thẳng chứa 2 cạnh đối) thẳng hàng nên ACHT là hình thang. (bổ đề hình thang quen thuộc)
\(\Rightarrow\) HT//AC \(\Rightarrow\) H, K, T thẳng hàng.
Lại có \(\widehat{CEH}=\widehat{CAH}\) (góc nội tiếp cùng chắn cung AH)
Mà \(\widehat{CAH}=\widehat{B}\) (cùng phụ với góc C)
\(\Rightarrow\widehat{CEH}=\widehat{B}\)
\(\Rightarrow\) Tứ giác BTEH nội tiếp \(\Rightarrow\widehat{BEH}=\widehat{BTH}\)
Mà \(\widehat{BTH}=90^o\) nên \(\widehat{BEH}=90^o\). Ta có đpcm.

a)Nối F với D : E với D ta có:
Xét tam giác FBC ta có
D là trung điểm BC(1)
Góc BFC=90 (2)
Từ (1)(2)=>FD là trung tuyến của tam giác FBC
=>BD=CD=DF(*)
Chứng minh tương tự tam giác EBC
=>DE=DC=DB(**)
Từ (*)(**)=>BD=CD=DF=DE=(1/2BC)
=>B;F;E;C thuộc đừng tròn
=>D là tâm của đường tròn
B) Do B;H;E nằm trên cùng 1 đừng thẳng => H ko thuộc đừng tròn
=>B;H;E;c ko thuộc đừng tròn

(Câu e không liên quan tới mấy câu trước, nhở)
Vẽ đường cao \(AL\). Khi đó \(AH.BC=AH\left(BL+CL\right)=AH.BL+AH.CL=2S_{AHB}+2S_{AHC}\)
Lập thêm 2 cái tương tự rồi cộng lại, phép màu sẽ xảy ra.
