Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hệ thức lượng: \(AH^2=BH.CH\)
Hai tam giác vuông BEH và HFC đồng dạng: \(\Rightarrow\dfrac{BE}{FH}=\dfrac{EH}{CF}\Rightarrow BE.CF=EH.FH\)
Hai tam giác vuông AEH và CFH đồng dạng \(\Rightarrow\dfrac{AH}{CH}=\dfrac{EH}{FH}\Rightarrow AH.FH-CH.EH=0\)
Hai tam giác vuông BEH và AFH đồng dạng \(\Rightarrow\dfrac{BH}{AH}=\dfrac{EH}{FH}\Rightarrow EH.AH-BH.FH=0\)
Ta có: \(\left(BE\sqrt{CH}+CF\sqrt{BH}\right)^2=BE^2.CH+CF^2.BH+2BE.CF.\sqrt{BH.CH}\)
\(=BE^2.CH+CF^2.BH+2BE.CF.AH\)
\(=\left(BH^2-EH^2\right)CH+\left(CH^2-FH^2\right)BH+2BE.CF.AH\)
\(=BH.CH\left(BH+CH\right)-EH^2.CH-FH^2.BH+2EH.FH.AH\)
\(=AH^2.BC+EH\left(AH.FH-EH.CH\right)+FH\left(AH.EH-FH.BH\right)\)
\(=AH^2.BC=\left(AH\sqrt{BC}\right)^2\)
\(\Rightarrow BE\sqrt{CH}+CF\sqrt{BH}=AH\sqrt{BC}\)

1: Xét tứ giác AEHF có góc AEH=góc AFH=góc FAE=90 độ
nên AEHF là hình chữ nhật
Suy ra: góc AEF=góc AHF=góc C(1)
Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MC
=>góc MAC=góc MCA(2)
Từ (1) và (2) suy ra góc AEF=góc C
2: Tham khảo:
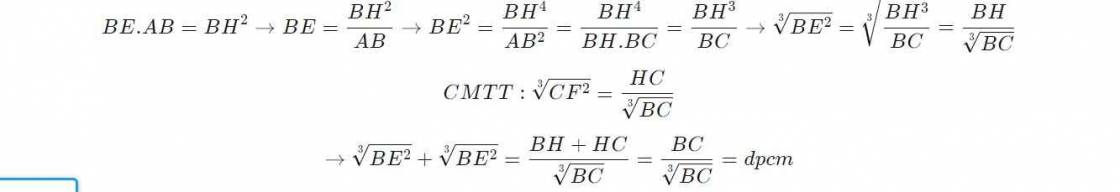

câu a) bn có thể vào câu hỏi tương tự xem, cái này làm vui thôi
Ta có: \(BN=\frac{BH^2}{AB};CM=\frac{CH^2}{AC};AB.AC=AH.BC;BH.CH=AH^2\)
\(\sqrt[3]{BC^2}=\sqrt[3]{BN^2}+\sqrt[3]{CM^2}\)
\(\Leftrightarrow\)\(BC^2=BN^2+CM^2+3\sqrt[3]{\left(BN.CM\right)^2}\left(\sqrt[3]{BN^2}+\sqrt[3]{CM^2}\right)\)
\(\Leftrightarrow\)\(BC^2=BH^2-NH^2+CH^2-MH^2+3\sqrt[3]{\left(\frac{\left(BH.CH\right)^2}{AB.AB}\right)^2}.\sqrt[3]{BC^2}\)
\(\Leftrightarrow\)\(BC^2=\left(BH^2+CH^2\right)-\left(NH^2+MH^2\right)+3\sqrt[3]{\left(\frac{AH^4}{AH.BC}\right)^2}.\sqrt[3]{BC^2}\)
\(\Leftrightarrow\)\(BC^2=\left(BH+CH\right)^2-2BH.CH-\left(NH^2+MH^2\right)+3\sqrt[3]{\frac{AH^6}{BC^2}}.\sqrt[3]{BC^2}\)
\(\Leftrightarrow\)\(BC^2=BC^2-2AH^2-AH^2+3AH^2\) ( do \(NH^2=AM^2\) )
\(\Leftrightarrow\)\(BC^2=BC^2\) ( luôn đúng )
\(\Rightarrow\)\(\sqrt[3]{BC^2}=\sqrt[3]{BN^2}+\sqrt[3]{CM^2}\) đúng
b) bằng một cách nào đó \(\Delta NBH\) đã đồng dạng với \(\Delta ABC\) ( có góc B chung ) \(\Rightarrow\)\(\frac{BN}{AB}=\frac{BH}{BC}\)
Tương tự: \(\Delta MHC~\Delta ABC\) ( có góc C chung ) \(\Rightarrow\)\(\frac{CM}{AC}=\frac{CH}{BC}\)
\(\Rightarrow\)\(\frac{BN}{AB}+\frac{CM}{AC}=\frac{BH+CH}{BC}=1\)
\(\Leftrightarrow\)\(BN.AC+CM.AB=AB.AB\)
\(\Leftrightarrow\)\(BN\sqrt{AC^2}+CM\sqrt{AB^2}=AB.AC\)
\(\Leftrightarrow\)\(BN\sqrt{CH.BC}+CM\sqrt{BH.BC}=AH.BC\)
\(\Leftrightarrow\)\(BN\sqrt{CH}+CM\sqrt{BH}=AH\sqrt{BC}\) ( chia 2 vế cho \(\sqrt{BC}\ne0\) ) đpcm

a: Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
b:
Xét tứ giác AEHF có \(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
nên AEHF là hình chữ nhật
=>AH=EF
Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot EB=HE^2\)
Xét ΔAHC vuông tại H có HF là đường cao
nên \(FA\cdot FC=FH^2\)
\(AE\cdot EB+FA\cdot FC=EH^2+FH^2=EF^2=AH^2\)
c: \(\dfrac{BE}{CF}=\dfrac{BH^2}{AB}:\dfrac{CH^2}{AC}=\dfrac{BH^2}{AB}\cdot\dfrac{AC}{CH^2}\)
\(=\dfrac{AB^4}{AC^4}\cdot\dfrac{AC}{AB}=\dfrac{AB^3}{AC^3}\)

a: Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\dfrac{BH}{CH}=\dfrac{AB^2}{AC^2}\)
b: \(\dfrac{BE}{CF}=\dfrac{BH^2}{AB}:\dfrac{CH^2}{AC}=\dfrac{BH^2}{AB}\cdot\dfrac{AC}{CH^2}\)
\(=\dfrac{BH^2}{CH^2}\cdot\dfrac{AC}{AB}=\dfrac{AB^4}{AC^4}\cdot\dfrac{AC}{AB}=\dfrac{AB^3}{AC^3}\)
e: \(BE\cdot CF\cdot BC\)
\(=\dfrac{HB^2}{AB}\cdot\dfrac{HC^2}{AC}\cdot BC\)
\(=\dfrac{AH^4}{AB\cdot AC}\cdot BC=\dfrac{AH^4}{AH\cdot BC}\cdot BC=AH^3\)
\(=EF^3\)
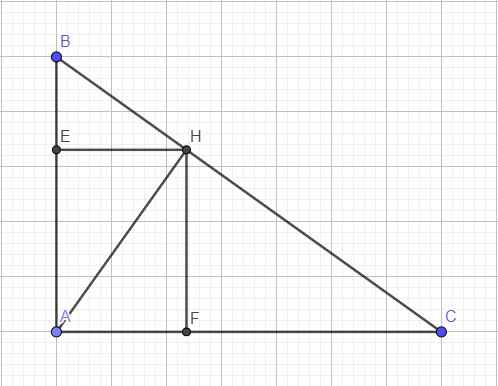
ta can cm\(\sqrt[3]{BE^2}+\sqrt[3]{CF^2}\) =\(\sqrt[3]{BC}\)
hay \(\sqrt[3]{\frac{BE^2}{BC^2}}+\sqrt[3]{\frac{CF^2}{BC^2}}=1\)
trong tam giác AHB \(BH^2=BE.BA\Rightarrow BE=\frac{BH^2}{BA}\Rightarrow BE^2=\frac{BH^4}{BA^2}\) (1)
ma trong tam giac ABC \(AB^2=BH.BC\)
thay vao (1) ta co \(BE^2=\frac{BH^4}{AB^2}=\frac{BH^4}{BH.BC}=\frac{BH^3}{BC}\Rightarrow\frac{BE^2}{BC^2}=\frac{BH^3}{BC^3}\)
\(\Rightarrow\sqrt[3]{\frac{BE^2}{BC^2}}=\frac{BH}{BC}\)
CM TUONG TU \(\sqrt[3]{\frac{CF^2}{BC^2}}=\frac{CH}{BC}\)
VAY \(\sqrt[3]{\frac{BE^2}{BC^2}}+\sqrt[3]{\frac{CF^2}{BC^2}}=\frac{HB}{BC}+\frac{CH}{BC}=1\)