Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

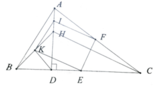
a, Chứng minh IFEK là hình bình hành có tâm O. Chứng minh IK ⊥ KE => IFEKlà hình chữ nhật => I,F,E,K cùng thuộc (O;OI)
b, Ta có: I D E ^ = 90 0 => Tam giác IDE vuông tại D
Chứng minh rằng KD ⊥ DF => ∆ KDF vuông

a: Xét (I) có
ΔAHC nội tiếp đường tròn
AC là đường kính
Do đó: ΔAHC vuông tại H
hay AH\(\perp\)BC

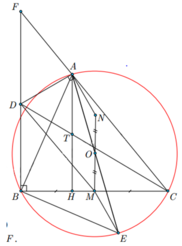
b) CD đi qua trung điểm của đường cao AH của D ABC
· Gọi F là giao của BD và CA.
Ta có BD.BE= BA.BM (cmt)
= > B D B A = B M B E = > Δ B D M ~ Δ B A E ( c − g − c ) = > B M D = B E A
Mà BCF=BEA(cùng chắn AB)
=>BMD=BCF=>MD//CF=>D là trung điểm BF
· Gọi T là giao điểm của CD và AH .
DBCD có TH //BD = > T H B D = C T C D (HQ định lí Te-let) (3)
DFCD có TA //FD = > T A F D = C T C D (HQ định lí Te-let) (4)
Mà BD= FD (D là trung điểm BF ) (5)
· Từ (3), (4) và (5) suy ra TA =TH ÞT là trung điểm AH .
ssdzsawrrrrrrt
Xét \(\Delta ABC\)có D và F lần lượt là trung điểm của AB và BC \(\Rightarrow\)DF là đường trung bình của \(\Delta ABC\)
\(\Rightarrow DF//AC\)
Mà \(AB\perp AC\Rightarrow DF\perp AB\Rightarrow\widehat{ADF}=90^0\)
Xét tứ giác ADHF có \(\widehat{ADF}=\widehat{AHF}\left(=90^0\right)\Rightarrow\)Tứ giác ADHF nội tiếp được đường tròn. \(\Rightarrow\)Đường tròn đi qua A, D, H đi qua F. (1)
Dễ dàng chứng minh EF là đường trung bình của \(\Delta ABC\)\(\Rightarrow EF//AB\)
Mà \(AB\perp AC\Rightarrow EF\perp AC\Rightarrow\widehat{AEF}=90^0\)
Xét tứ giác ADFE có \(\widehat{DAE}=\widehat{ADF}=\widehat{AEF}\left(=90^0\right)\Rightarrow\)Tứ giác ADFE là hình chữ nhật \(\Rightarrow\)A,D,F,E cùng thuộc một đường tròn \(\Rightarrow\)Đường tròn đi qua A,D,F cũng đi qua E. Mà đường tròn đi qua A,D,F chính là đường tròn đi qua A,D,H nên đường tròn đi qua A,D,H đi qua E. (2)
Từ (1) và (2) \(\Rightarrowđpcm\)