Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=36+64=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC có BD là phân giác
nên \(\dfrac{DA}{AB}=\dfrac{DC}{BC}\)
=>\(\dfrac{DA}{6}=\dfrac{DC}{10}\)
=>\(\dfrac{DA}{3}=\dfrac{DC}{5}\)
mà DA+DC=AC=8cm(D nằm giữa A và C)
nên \(\dfrac{DA}{3}=\dfrac{DC}{5}=\dfrac{DA+DC}{3+5}=\dfrac{8}{8}=1\)
=>\(DA=3\cdot1=3cm;DC=5\cdot1=5cm\)
b: ΔABC vuông tại A
mà AM là đường trung tuyến
nên \(AM=MB=MC=\dfrac{BC}{2}=5\left(cm\right)\)
mà DC=5cm
nên CM=CD
Xét ΔCDI và ΔCMI có
CD=CM
\(\widehat{DCI}=\widehat{MCI}\)
CI chung
Do đó: ΔCDI=ΔCMI
=>\(\widehat{CID}=\widehat{CIM}\) và \(\widehat{IMC}=\widehat{IDC}\)(3)
Ta có: \(\widehat{IDC}=\widehat{BAD}+\widehat{ABD}\)(góc IDC là góc ngoài tại đỉnh D của ΔABD)
nên \(\widehat{IDC}=\widehat{BAD}+\widehat{ABD}=90^0+\widehat{ABD}\)(2)
Xét ΔBIM có \(\widehat{IMC}\) là góc ngoài tại đỉnh M
nên \(\widehat{IMC}=\widehat{MIB}+\widehat{MBI}\left(1\right)\)
Từ (1),(2),(3) suy ra \(\widehat{MIB}+\widehat{MBI}=90^0+\widehat{ABD}\)
mà \(\widehat{MBI}=\widehat{ABD}\)
nên \(\widehat{MIB}=90^0\)

a) Xét tam giác ABC vuông tại A có:
* \(BC^2=AB^2+AC^2\)(định lý Py-ta-go)
\(< =>10^2=6^2+AC^2\)
\(< =>AC^2=100-36\)
\(< =>AC=\sqrt{64}\)
\(< =>AC=8\)
Chu vi tam giác ABC là : \(AB+AC+BC=6+10+8=24\left(cm\right)\)
Diện tích tam giác ABC là: \(\frac{AB.AC}{2}=\frac{6.8}{2}=24\left(cm^2\right)\)
b) Ta có: BD là phân giác của góc B (gt)
=> \(\frac{DA}{DC}=\frac{BA}{BC}\)(tính chất đường phân giác trong 1 tam giác)
Mà \(\frac{BA}{BC}=\frac{6}{10}=\frac{3}{5}\)
=>\(\frac{DA}{DC}=\frac{3}{5}\)
c) Xét tam giác ABI có:
* BD là phân giác góc B (gt)
* BD là đường cao (AI vuông góc BD)
=> Tam gi1c ABI cân tại B
=> BA = BI (tính chất)
Xét tam giác ABD và tam giác IBD có:
*AB = IB (cmt)
*Góc ABD = Góc IBD (BD là phân giác)
*BD là cạnh chung
=> tam giác ABD = tam giác IBD (c-g-c)
=> Góc BAD = Góc BID (tính chất)
Mà góc BAD = 90 độ (tam giác ABC vuông tại A)
=> Góc BID = 90 độ

a: AD là phân giác
=>BD/AB=CD/AC
=>BD/6=3/9=1/3
=>BD=2cm
b: \(S_{ABC}=\dfrac{1}{2}\cdot3\cdot\left(2+3\right)=\dfrac{3}{2}\cdot5=\dfrac{15}{2}\left(cm^2\right)\)

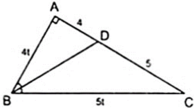
Áp dụng tính chất đường phân giác BD của tam giác
ABC, ta có:
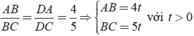 với t > 0
với t > 0
Áp dụng định lý Py – ta – go ta có:
B C 2 = A C 2 + A B 2 hay ( 5 t ) 2 = 9 2 + ( 4 t ) 2 ⇔ ( 3 t ) 2 = 9 2 ⇒ t = 3 (vì t > 0 )
Khi đó: AB = 12cm, BC = 15cm

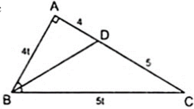
Áp dụng tính chất đường phân giác BD của tam giác ABC, ta có:
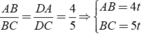 với t > 0
với t > 0
Áp dụng định lý Py – ta – go ta có:

Khi đó: AB = 12cm, BC = 15cm


Theo định lí Pytago tam giác ABC vuông tại A
\(AC=\sqrt{BC^2-AB^2}=12cm\)
Vì BD là pg \(\dfrac{AB}{BC}=\dfrac{AD}{DC}\Rightarrow\dfrac{DC}{BC}=\dfrac{AD}{AB}\)
Theo tc dãy tỉ số bằng nhau ta có
\(\dfrac{DC}{BC}=\dfrac{AD}{AB}=\dfrac{12}{24}=\dfrac{1}{2}\Rightarrow DC=\dfrac{15}{2}cm;DA=\dfrac{9}{2}cm\)
Cảm mơn bạn nhiều nha