Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác AMB và tam giác CMK:
+ AM = MC (M là trung điểm của AC).
+ BM = KM (gt).
+ \(\widehat{AMB}=\widehat{CMK}\) (đối đỉnh).
\(\Rightarrow\) Tam giác AMB = Tam giác CMK (c - g - c).
b) Ta có: \(\widehat{BAM}=\widehat{KCM}\) (Tam giác AMB = Tam giác CMK).
\(\Rightarrow\) AB // CK (dhnb).

a: Xét ΔAMB và ΔCMD có
MA=MC
\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)
MB=MD
Do đó: ΔAMB=ΔCMD
b: ta có: ΔAMB=ΔCMD
=>\(\widehat{MAB}=\widehat{MCD}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
c: Xét ΔIBM và ΔKDM có
IB=KD
\(\widehat{IBM}=\widehat{KDM}\)(hai góc so le trong, AB//CD)
BM=MD
Do đó: ΔIBM=ΔKDM
=>\(\widehat{IMB}=\widehat{KMD}\)
mà \(\widehat{IMB}+\widehat{IMD}=180^0\)(hai góc kề bù)
nên \(\widehat{KMD}+\widehat{IMD}=180^0\)
=>I,M,K thẳng hàng

UKM THÌ CÓ BÀI TỰA VẬY BẠN SO ĐC CHỨ
a) Xét AIM và BIC có:IA = IB (do I là trung điểm của AB);AIM BIC(hai góc đối đỉnh);IM = IC (giảthiết).Do đó AIM = BIC (c.g.c)Suy ra AM = BC (hai cạnh tương ứng) và MAI CBI(hai góc tương ứng) Mà MAI, CBIlà hai góc ởvịtrí so le trong nên AM // BC.b) Xét ANE và CBE có:EA = EC (do E là trung điểm của AC);AEN CEB(hai góc đối đỉnh);EN= EB(giảthiết).Do đó ANE = CBE (c.g.c)Suy ra NAE BCE(hai góc tương ứng)Mà NAE, BCElà hai góc ởvịtrí so le trong nên AN// BC.c) Ta có AM // BC (theo câu a) và AN // BC (theo câu b)Do đó qua điểm A có hai đường thẳng song song với BC nên theo tiên đềEuclid, hai đường thẳng AM và AN trùng nhau hay ba điểm A, M, N thẳng hàng.Lại có ANE = CBE (theo câu b) nên AN = CB (hai cạnh tương ứng)Mặt khác AM = BC (theo câu a)Do đó AM = AN (cùng bằng BC) Mà ba điểm A, M, N thẳng hàng nên A là trung điểm của MN.a: Xét ΔAMB và ΔCMD có
MA=MC
góc AMB=góc CMD
MB=MD
Do đó: ΔAMB=ΔCMD
b: Xét tứ giác ABCD có
M là trung điểm chung của AC và BD
nên ABCD là hình bình hành
=>AB//CD và AB=CD
c: Xét tứ giác AKBC có
N là trung điểm chung của AB và KC
nên AKBC là hình bình hành
=>AK//BC
mà AD//BC
nên D,A,K thẳng hàng

a: Xét ΔAMB và ΔCMD có
MA=MC
\(\widehat{AMB}=\widehat{CMD}\)
MB=MD
Do đó: ΔAMB=ΔCMD
b: Xét ΔMAD và ΔMCB có
MA=MC
\(\widehat{AMD}=\widehat{CMB}\)
MD=MB
Do đó: ΔMAD=ΔMCB
=>\(\widehat{MAD}=\widehat{MCB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//BC
c: Xét ΔNAK và ΔNBC có
NA=NB
\(\widehat{ANK}=\widehat{BNC}\)(hai góc đối đỉnh)
NK=NC
Do đó; ΔNAK=ΔNBC
=>\(\widehat{NAK}=\widehat{NBC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AK//BC
Ta có: AD//BC
AK//BC
AK,AD có điểm chung là A
Do đó: D,A,K thẳng hàng
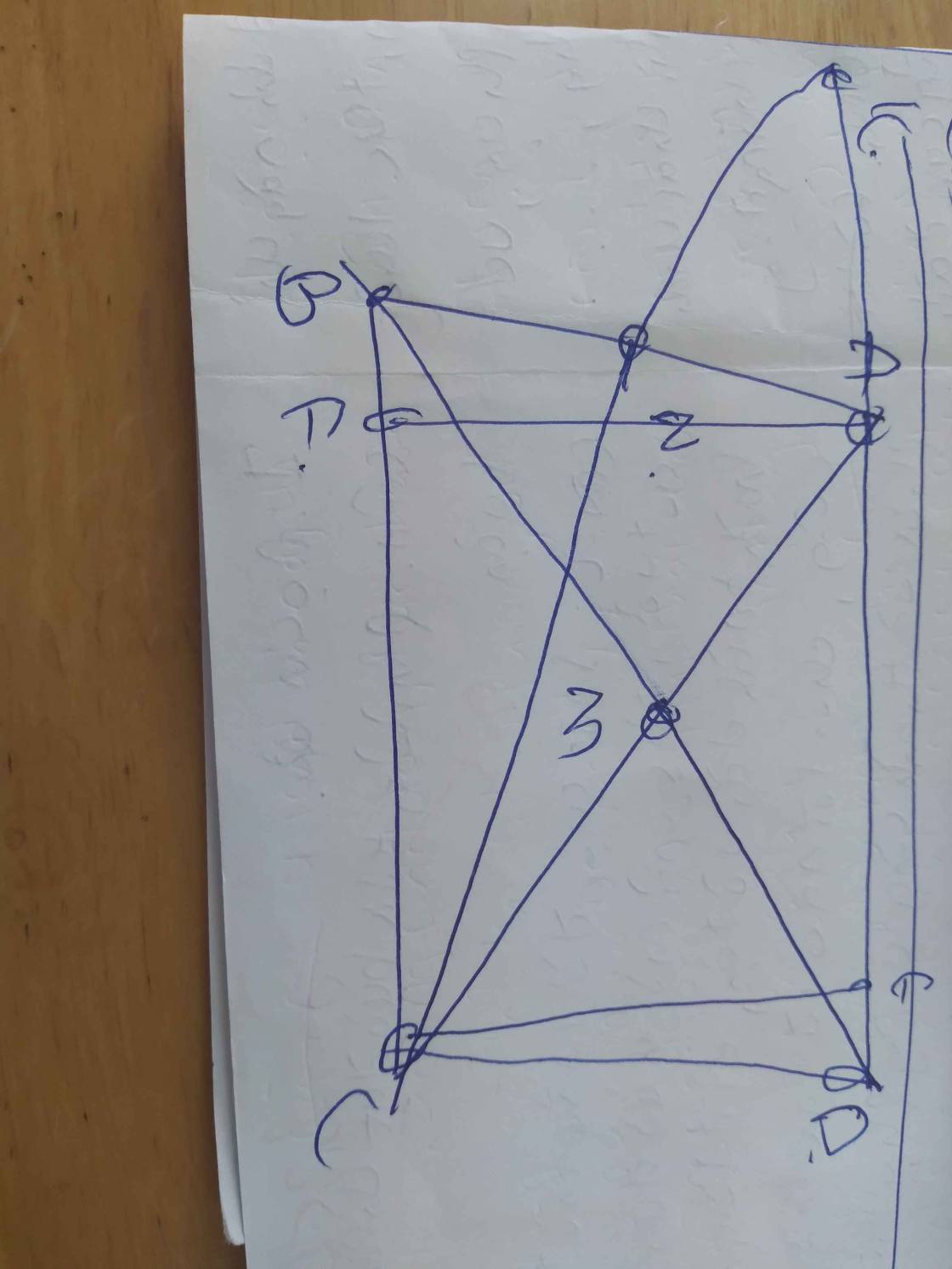


b,Xét tam giác AMB và tam giác CMK có:
AM=MB(M là trung điểm của AC)
góc AMB=góc CMK
BM=KM(gt)
=> TAm giác AMB=tam giác CMK(c.g.c)
=> góc BAM=góc KCM (hai cạnh tương ứng)
Vậy KC vuông góc với AC
P/s : Học giỏi^^