Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔADB và ΔADC có
AB=AC
góc BAD=góc CAD
AD chung
=>ΔABD=ΔACD
b: Xét ΔAMD vuông tại M và ΔAND vuông tại N có
AD chung
góc MAD=góc NAD
=>ΔMAD=ΔNAD
=>MD=DN
=>ΔDMN cân tại D

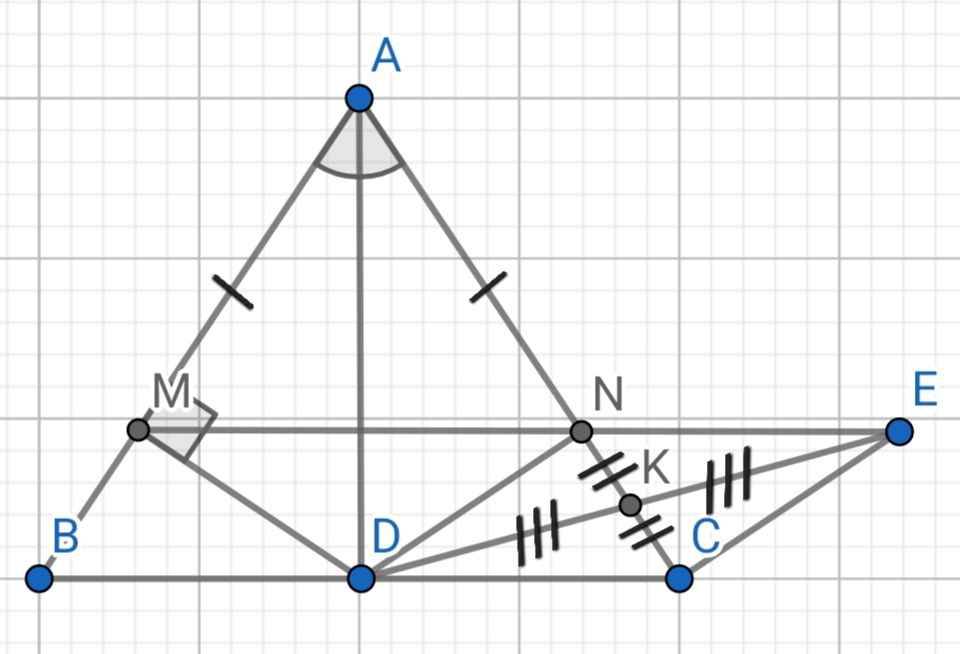 a) Do AD là tia phân giác của ∠BAC (gt)
a) Do AD là tia phân giác của ∠BAC (gt)
⇒ ∠BAD = ∠CAD
Do ∆ABC cân tại A
⇒ AB = AC
Xét ∆ABD và ∆ACD có:
AB = AC (cmt)
∠BAD = ∠CAD (cmt)
AD là cạnh chung
⇒ ∆ABD = ∆ACD (c-g-c)
⇒ BD = CD
⇒ D là trung điểm của BC (1)
Do ∆ABD = ∆ACD (cmt)
⇒ ∠ADB = ∠ADC (hai góc tương ứng)
Mà ∠ADB + ∠ADC = 180⁰ (kề bù)
⇒ ∠ADB = ∠ADC = 180⁰ : 2 = 90⁰
⇒ AD ⊥ BC (2)
Từ (1) và (2) ⇒ AD là đường trung trực của BC
b) Sửa đề: Chứng minh ∆ADM = ∆ADN
Do ∠BAD = ∠CAD (cmt)
⇒ ∠MAD = ∠NAD
Xét ∆ADM và ∆ADN có:
AD là cạnh chung
∠MAD = ∠NAD (cmt)
AM = AN (gt)
⇒ ∆ADM = ∆ADN (c-g-c)
⇒ ∠AMD = ∠AND = 90⁰ (hai góc tương ứng)
⇒ DN ⊥ AN
⇒ DN ⊥ AC
d) Do K là trung điểm của CN (gt)
⇒ CK = KN
Xét ∆DKC và ∆EKN có:
CK = KN (cmt)
∠DKC = ∠EKN (đối đỉnh)
KD = KE (gt)
⇒ ∆DKC = ∆EKN (c-g-c)
⇒ ∠KDC = ∠KEN (hai góc tương ứng)
Mà ∠KDC và ∠KEN là hai góc so le trong
⇒ EN // CD
⇒ EN // BC (3)
∆AMN có:
AM = AN (gt)
⇒ ∆AMN cân tại A
⇒ ∠AMN = (180⁰ - ∠MAN) : 2
= (180⁰ - ∠BAC) : 2 (4)
∆ABC cân tại A (gt)
⇒ ∠ABC = (180⁰ - ∠BAC) : 2 (5)
Từ (4) và (5) ⇒ ∠AMN = ∠ABC
Mà ∠AMN và ∠ABC là hai góc đồng vị
⇒ MN // BC (6)
Từ (3) và (6) kết hợp với tiên đề Euclide ⇒ M, N, E thẳng hàng

a, xét tam giác AMD và tam giác AND có : AD chung
^MAD = ^NAD do AD là pg của ^BAC (gt)
^AMD = ^AND = 90
=> tam giác AMD = tam giác AND (ch-gn)
b, xét tam giác BMD vuông tại M => ^B + ^MDB = 90 (đl)
^B = 30 (gt)
=> ^MDB = 60
tương tự tính đượng ^NDC = 60
có : ^MDB + ^NDC + ^MDN = 180
=> ^MDN = 60
c, AB = AC do tam giác ABC cân tại A (gt)
AM = AN do tam giác AMD = tam giác AND (Câu a)
AB = AM + BM
AC = AN + NC
=> BM = NC
xét tam giác DMB và tam giác DNC có : ^B = ^C
^DMB = ^DNC = 90
=> tam giác DMB = tam giác DNC (cgv-gnk)

bạn ơi câu này phải là trên tia đối của BA và CA lấy 2 điểm D và E sao cho BD=CE
a) Vì ∆ABC cân tại A
=> ABC = \(\frac{180°-BAC}{2}\)
Vì ∆ABC cân tại A
=> AB = AC
Mà BD = CE
=> AB + BD = AC + CE
Hay AD = AE
=> ∆ADE cân tại A
=> ADE = \(\frac{180°-BAC}{2}\)
=> ADE = ABC
Mà 2 góc này ở vị trí đồng vị
=> BC //DE
b) Vì BC //DE
=> BCED là hình thang
Vì ∆ADE cân tại A=> ADE = AED
=> BCED là hình thang cân
=> BD = CE
=> BDE = CED
Vì BC //DE
=> MN//DE
=> NMD = MDE = 90°
=> MNE = NED = 90°
=> MDE = NED
Mà MDE = MDB + BDE
NED = NEC + CED=
=> NEC = MDB
Xét ∆ vuông BMD và ∆ vuông CNE ta có :
BD = CE
NEC = MDB (cmt)
=> ∆BMD = ∆CNE ( cgv-gn)
c) Ta thấy ADB là góc ngoài ∆ABC tại đỉnh B
=> BAC + ABC = AMB
Ta thấy : ANC là góc ngoài ∆ABC tại đỉnh C
=> BAC + ACB = ANC
Mà ABC = ACB ( ∆ABC cân tại A)
=> AMB = ANC
=> ∆AMN cân tại A
a: góc ABC=90-30=60 độ
góc DBM=180-45-60=75 độ
góc DCN=45+30=75 độ
b: Xét ΔDNC vuông tại N và ΔDBM vuông tại M có
DC=DB
góc DCN=góc DBM
=>ΔDNC=ΔDBM
=>DM=DN
c: Xét tứ giác AMDN có
góc AMD=góc AND=góc MAN=90 độ
DM=DN
=>AMDN là hình vuông
=>AD là phân giác của góc BAC