Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
b: Xét ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền AC
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=10^2-6^2=64\)
=>AC=8(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AH\cdot BC=AB\cdot AC\\AB^2=BH\cdot BC\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AH=\dfrac{6\cdot8}{10}=4,8\left(cm\right)\\BH=\dfrac{6^2}{10}=3,6\left(cm\right)\end{matrix}\right.\)
b: ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra AE*AB=AF*AC
=>AE/AC=AF/AB
Xét ΔAEF vuông tại A và ΔACB vuông tại A có
AE/AC=AF/AB
Do đó: ΔAEF đồng dạng với ΔACB
c: Xét ΔBAC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{CB}\)
=>\(\dfrac{AB}{AD}=\dfrac{CB}{CD}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AB}{AD}=\dfrac{CB}{CD}=\dfrac{AB+BC}{AD+CD}=\dfrac{AB+BC}{AC}\)(1)
ΔBAD vuông tại A có
\(cotABD=\dfrac{AB}{AD}\)(2)
BD là phân giác của góc ABC
=>\(\widehat{ABD}=\widehat{DBC}\left(3\right)\)
Từ (1),(2),(3) suy ra \(cotDBC=\dfrac{AB+BC}{AC}\)
Gọi AM cắt DE tại I
Theo tính chất hình chữ nhật ADHE : \(\widehat{E_1}=\widehat{HAC}=\widehat{MBA};\widehat{A_1}=\widehat{D_1}=\widehat{AHE}=\widehat{MCA}\)
\(\Rightarrow\widehat{A_1}=\widehat{ACM}\Rightarrow\Delta ACM\)cân tại M \(\Rightarrow MA=MC\)(*)
Do \(\Delta AID\)vuông tại I suy ra
\(\widehat{DAM}+\widehat{D_1}=90^0\Leftrightarrow\widehat{DAM}+\widehat{DAH}=90^0\left(1\right)\)
\(\widehat{ABM}+\widehat{DAH}=90^0\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{DAM}=\widehat{ABM}\)
\(\Rightarrow\Delta ABM\)cân tại M \(\Rightarrow MA=MB\)(**)
Từ (*);(**) suy ra MB=MC hay M là trung điểm BC . Do MF//AC suy ra
\(\widehat{MFC}=\widehat{ACF}\)
Mà
\(\widehat{ACF}=\widehat{MCF}\Rightarrow\widehat{MFC}=\widehat{MCF}\Rightarrow\Delta MFC\)cân tại M suy ra MC=MF
Mà MB=MC suy ra 
\(\Delta BFC\) có FM là trung tuyến 
\(FM=\frac{1}{2}BC\Rightarrow\) \(\Delta BFC\)vuông tại F hay 
\(BF\perp CF\left(đpcm\right)\)
Câu 1:
a: Xét ΔAHB vuông tạiH có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
b: \(BC=\sqrt{4^2+6^2}=2\sqrt{13}\left(cm\right)\)
\(AH=\dfrac{4\cdot6}{2\sqrt{13}}=\dfrac{12}{\sqrt{13}}\left(cm\right)\)
\(AE=\dfrac{AH^2}{AC}=\dfrac{144}{13}:6=\dfrac{24}{13}\left(cm\right)\)
a: \(AB=\sqrt{3\cdot15}=3\sqrt{5}\left(cm\right)\)
\(AC=\sqrt{12\cdot15}=6\sqrt{5}\left(cm\right)\)
b: \(\dfrac{HF}{HE}=\dfrac{AE}{AF}=\dfrac{AH^2}{AB}:\dfrac{AH^2}{AC}=\dfrac{AC}{AB}=2\)
=>HF=2HE
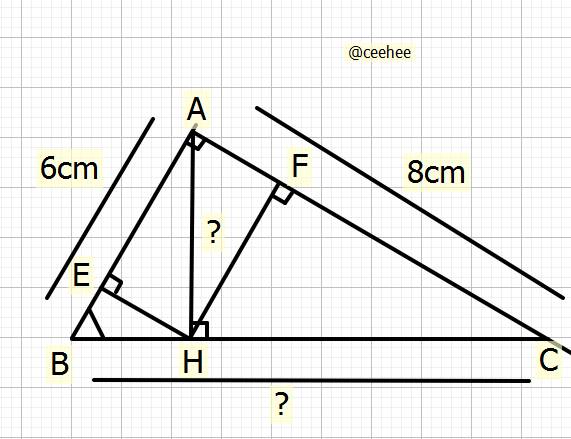
`a)` Tỉ số lượng giác góc `B` của \(\Delta ABC\)
\(SinB=\dfrac{AC}{BC}\\ CosB=\dfrac{AB}{BC}\\ TanB=\dfrac{AC}{AB}\\ CotB=\dfrac{AB}{AC}\)
`b)` Tính `BC,AH`
Xét \(\Delta ABC\) vuông tại `A`, đường cao `AH`
Ta có: \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\left(htl\right)\)
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{6^2}+\dfrac{1}{8^2}\\ \Rightarrow\dfrac{1}{AH^2}=\dfrac{25}{576}\\ \Rightarrow AH^2=\dfrac{576\cdot1}{25}=23,04\\ \Rightarrow AH=\sqrt{23,04}=4,8cm\)
Ta có: \(AB\cdot AC=AH\cdot BC\left(htl\right)\)
\(\Rightarrow6\cdot8=4,8\cdot BC\\ \Rightarrow48=4,8\cdot BC\\ \Rightarrow BC=\dfrac{48}{4,8}\\ \Rightarrow BC=10cm\)
Vậy: `AH = 4,8cm; BC= 10cm`
`c)` C/m: `AE * AB = AF * AC`
Xét \(\Delta AHB\) vuông tại `H`, đường cao `HE`
Ta có: \(AH^2=AE\cdot AB\left(htl\right)\) `(1)`
Xét \(\Delta AHC\) vuông tại `H`, đường cao `HF`
Ta có: \(AH^2=AF\cdot AC\left(htl\right)\) `(2)`
Từ `(1)` và `(2)` \(\Rightarrow AH^2=AH^2\)
\(\Rightarrow AE\cdot AB=AF\cdot AC\left(=AH^2\right).\)