Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAHB vuông tại H và ΔCHA vuông tạiH có
góc HAB=góc HCA
=>ΔAHB đồng dạng với ΔCHA
c: BK là phân giác
=>AK/CK=BA/BC
ΔAHC có AD là phân giác
nên DH/CD=AH/AC=BA/BC
=>DH/CD=AK/CK
=>KD//AH

a) Xét ΔAHB vuông tại H và ΔCAB vuông tại A có
\(\widehat{CBA}\) chung
Do đó: ΔAHB\(\sim\)ΔCAB(g-g)

Lời giải:
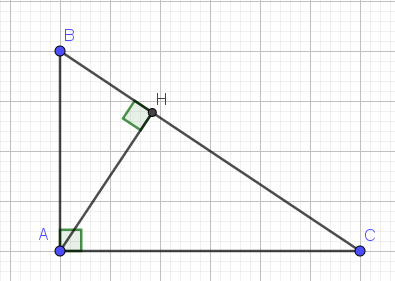
a. Xét tam giác $AHB$ và $CHA$ có:
$\widehat{AHB}=\widehat{CHA}=90^0$
$\widehat{HAB}=\widehat{HCA}$ (cùng phụ với $\widehat{HAC}$)
$\Rightarrow \triangle AHB\sim \triangle CHA$ (g.g)
b.
$BH=\sqrt{AB^2-AH^2}=\sqrt{15^2-12^2}=9$ (cm)
Từ tam giác đồng dạng phần a suy ra $CH=\frac{AH^2}{BH}=\frac{12^2}{9}=16$ (cm)
$AC=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=20$ (cm)

Tam giác ABC vuông
=>
BC2 = AB2 + AC2
AH.BC = AB.AC
=>
BC2 = 225 + AC2
12BC = 15AC
Thay BC = 15AC/12 vào pt trên
=>
81AC2 = 32400
=> AC2 = 400
=> AC = 20cm
=> BC = 25cm
BH = \(\sqrt{AB^2-AH^2}\)= \(\sqrt{15^2-12^2}\)= 9
Ta có:
\(\widehat{AHB}\) = \(\widehat{CHA}\)= 90o (1)
cos (\(\widehat{ABH}\)) = \(\frac{BH}{AB}\)= \(\frac{9}{15}\)= \(\frac{3}{5}\)
cos (\(\widehat{CAH}\)) = \(\frac{AH}{AC}\)= \(\frac{12}{20}\)= \(\frac{3}{5}\)
=> \(\widehat{ABH}\)= \(\widehat{CAH}\)(2)
(1), (2) => Tam giác AHB đồng dạng CHA

Xét ΔAHB vuông tại H và ΔCHA vuông tại H có
góc HAB=góc HCA
=>ΔAHB đồng dạng với ΔCHA

A B C H D E
a, Xét tam giác AHB và tam giác CHA ta có :
^AHB = ^CHA = 900
^ABH = ^CAH ( cùng phụ ^BAH )
Vậy tam giác AHB ~ tam giác CHA ( g.g )
b, Xét tam giác AEB và tam giác DAB ta có
^AEB = ^DAB = 900
^B _ chung
Vậy tam giác AEB ~ tam giác DAB ( g.g )
Giúp mik ik mak