Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
Xét tg vuông ABC có
\(AB=\sqrt{CA^2+CB^2}\) (pitago)
\(\Rightarrow AB=\sqrt{4^2+3^2}=5cm\)
\(CM=\dfrac{1}{2}AB\) ( Trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
\(\Rightarrow CM=\dfrac{1}{2}.5=2,5cm\)
b.
Xét tứ giác ACMK có
IA=IM (gt); IC=IK (gt) => ACMK là hbh (Tứ giavs có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
c.
\(AC\perp BC\Rightarrow EC\perp BC\)
\(MD\perp BC\)
=> EC//MD (1)
\(BC\perp AC\Rightarrow DC\perp AC\)
\(ME\perp AC\)
=> DC//ME (2)
Từ (1) và (2) => ADME là hbh (Tứ giác có các cặp cạnh đối //)
Mà \(\widehat{C}=90^o\)
=> CDME là HCN (Hình bình hành có 1 góc vuông là HCN)
d.
ACMK là hbh (cmt) => AK=MC (cạnh đối hbh) (3)
Xét hình chữ nhật CDME
MC=DE (đường chéo HCN) (4)
Từ (3) và (4) => DE=AK
e.
DE=MC (cmt)
DE ngắn nhất khi MC ngắn nhất
MC ngắn nhất khi \(MC\perp AB\) (Khoảng cách nhỏ nhất từ 1 điểm đến 1 đường thẳng chính là khoảng cách từ điểm đã cho đến điểm giao của đường thẳng vuông góc với đường thẳng cho trước đi qua điểm đã cho )
=> DE ngắn nhất khi M là giao của đường thẳng vuông góc với AB đi qua C

a: Xét ΔMBE vuông tại E và ΔNCF vuông tại F có
MB=CN
\(\widehat{MBE}=\widehat{NCF}\left(=\widehat{ACB}\right)\)
Do đó: ΔMBE=ΔNCF
Suy ra: ME=NF
Xét ΔMEI vuông tại E và ΔNFI vuông tại F có
ME=NF
\(\widehat{EMI}=\widehat{FNI}\)
Do đó: ΔMEI=ΔNFI\(\left(cgv-gnk\right)\)
Suy ra: IE=IF
b: Ta có: CD=CN
mà CN=MB
nên MB=DC
Xét ΔBAC có
\(\dfrac{MB}{BA}=\dfrac{CD}{AC}\)
nên MD//BC
Xét tứ giác BMDC có MD//BC
nên BMDC là hình thang
mà \(\widehat{MBC}=\widehat{DCB}\)
nên BMDC là hình thang cân

a) Vì O cách đều 3 cạnh của tam giác nên OD = OE = OF
Áp dụng định lý Pytago vào tam giác vuông OBF và tam giác vuông ODB ta có:
BF=√OB2−OF2BF=OB2−OF2
BD=√OB2−OD2BD=OB2−OD2
Mà OF = OD nên BF = BD.
Tương tự áp dụng định lý Pytago vào tam giác vuông OEC và tam giác vuông ODC suy ra CE = CD
∆BAM có AB = BM nên ∆BAM là tam giác cân tại B ⇒ˆBAM=ˆBMA⇒BAM^=BMA^
Xét ∆BAM có BF = BD, BA = BM nên theo định lý Ta – lét ta có :
BFBA=BDBM⇒DF//AM⇒BFBA=BDBM⇒DF//AM⇒ DFAM là hình thang
Hình thang DFAM có ˆFAM=ˆAMDFAM^=AMD^ nên DFAM là hình thang cân
⇒{MF=ADAF=MD⇒{MF=ADAF=MD
∆ANC có AC = CN nên ∆ANC cân tại C⇒ˆCAN=ˆCNA⇒CAN^=CNA^
Xét ∆ANC có CE = CD, CA = CN nên theo định lý Ta – lét ta có :
CECA=CDCN⇒DE//AN⇒CECA=CDCN⇒DE//AN⇒ DEAN là hình thang
Hình thang DEAN có ˆCAN=ˆCNACAN^=CNA^ nên DEAN là hình thang cân
⇒{NE=ADAE=ND⇒{NE=ADAE=ND
⇒MF=NE⇒MF=NE
b) Xét ∆OEA và ∆ODN ta có :
⎧⎪⎨⎪⎩OE=ODˆOEA=ˆODNEA=DN{OE=ODOEA^=ODN^EA=DN⇒ΔOEA=ΔODN(c−g−c)⇒ON=OA⇒ΔOEA=ΔODN(c−g−c)⇒ON=OA
Xét ∆OAF và ∆OMD ta có :
⎧⎪⎨⎪⎩AF=MDˆOFA=ˆODMOF=OD{AF=MDOFA^=ODM^OF=OD⇒ΔOAF=ΔODM(c−g−c)⇒OA=OM⇒ΔOAF=ΔODM(c−g−c)⇒OA=OM
⇒OM=ON⇒OM=ON hay ∆MON cân tại O.

Bài 2:
a) Xét tam giác BMC và tam giác MCN có:
Chung đường cao hạ từ M xuống BN, 2 đáy BC=CN
\(\Rightarrow S_{BMC}=S_{MCN}\)
\(\Rightarrow S_{BMN}=2S_{BMC}\)(1)
Xét tam giác ABC và tam giác BMC có:
Chung đường cao hạ từ C xuống đường thẳng AM , 2 đáy AB=BM
\(\Rightarrow S_{ABC}=S_{BMC}\)(2)
Từ (1) và (2) \(\Rightarrow S_{BMN}=2S_{ABC}\)
CMTT \(S_{APM}=2S_{ABC};S_{PCN}=2S_{ABC}\)
\(\Rightarrow S_{PMN}=S_{PCN}+S_{APM}+S_{BMN}+S_{ABC}\)
\(=7S_{ABC}\left(đpcm\right)\)
Bài 3:

Áp dụng tính chất 2 tam giác có chung đường cao thì tỉ số diện tích bằng tỉ số 2 đáy tương ứng với đường cao đó, ta có:
\(BP=\frac{1}{3}BC\Rightarrow S_{ABP}=\frac{1}{3}S_{ABC}\)
Tương tự có \(\hept{\begin{cases}S_{BMC}=\frac{1}{3}S_{ABC}\\S_{CAN}=\frac{1}{3}S_{ABC}\end{cases}}\)
\(\Rightarrow S_{ABP}+S_{BMC}+S_{CAN}=S_{ABC}\)
\(\Rightarrow S_{ANE}+S_{BNEF}+S_{BFP}+S_{BFP}+S_{CPFI}+S_{CMI}+S_{CMI}+S_{MIEA}+S_{ANE}\)
\(=S_{ANE}+S_{BNEF}+S_{CPFI}+S_{BFP}+S_{CPFI}+S_{CMI}+S_{MIEA}+S_{EFI}\)
\(\Rightarrow S_{ANE}+S_{BFP}+S_{CMI}=S_{EFI}\left(đpcm\right)\)

Đề sai rồi bạn ơi! "Tam giác ABC" không phải "tam giác ABCD"
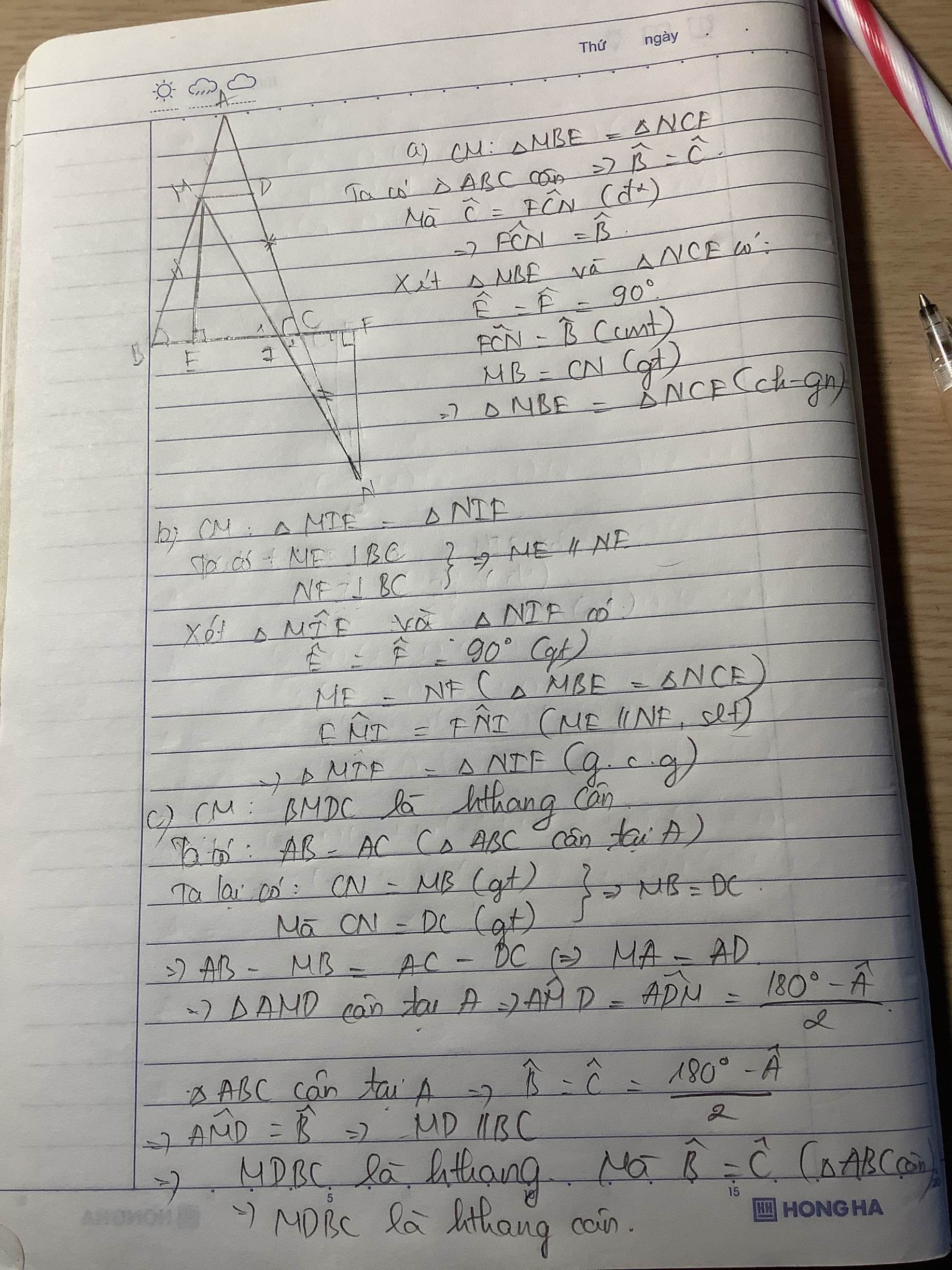
Xét tam giác ABC có
\(\begin{array}{l}\frac{{CM}}{{CA}} = \frac{1}{4}\\\frac{{CN}}{{CB}} = \frac{{1,25}}{5} = \frac{1}{4}\\ \Rightarrow \frac{{CM}}{{CA}} = \frac{{CN}}{{CB}}\end{array}\)
\( \Rightarrow MN\parallel AB\) (Định lý Thales đảo)
Mà \(AB \bot AC\) nên \(MN \bot AC\) hay tam giác MNC vuông tại M
Xét tam giác MNC vuông tại M có: \(MC = 1,\,\,NC = 1,25\).
Theo định lý Pytago ta có:
\(\begin{array}{l}M{N^2} + M{C^2} = N{C^2}\\\,\,\,\,\,\,\,M{N^2} + {1^2} = 1,{25^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,M{N^2} = 1,{25^2} - {1^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,M{N^2} = 0,5625\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,MN = 0,75\end{array}\)
Vậy MN = 0,75.