Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chú ý tam giác ABD cân tại B nên BM là đường phân giác cũng là đường cao, từ đó B M ⊥ A D .
b) Chú ý AK, BM, DH là ba đường cao của tam giác AMD.
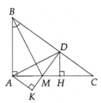

a, Xét tam giác BAD và tam giác BKD có :
BD : cạnh chung
BA = BK
Góc ABD = Góc DBK
==> Tam giác ABD = Tam giác KBD ( C - G - C )
==> AD = DK ( đpcm )
b, Xét tam giác ADE và tam giác KDC có :
AD = DK
Góc ADE = Góc KDC
Góc DAE = Góc DKC
==> Tam giác ADE = Tam giác KDC ( G - C - G )
c, Xét tam giác BAM và tam giác BKM có :
BM : cạnh chung
BA = BK
Góc ABM = Góc MBK
==> Tam giác ABM = Tam giác KBM ( C - G - C )
==> Góc BMA = Góc BMK Mà Góc AMK = 180 độ
==> Góc BMA = Góc BMK = 90 độ
==> AK vuông góc với BD
Ta có hình vẽ
Tớ chỉ vẽ hình thôi còn bài tự làm nhé! g
Gợi ý:
a) trước tiên ta xét Tam giác chứa cạnh AD và DK
Còn Muốn CM EK vuông góc vói BC thì CM nó tạo thành một góc 90 độ
b) chúng minh theo các trường hợp (c.g.c) (g.c.g) (c.c.c)

A B C D E K N
XÉT TAM GIÁC ABD VÀ TAM GIÁC AED
BA=EA ( GT)
\(\widehat{BAD}=\widehat{EAD}\)( GT)
AD-CẠNH CHUNG
=> TAM GIÁC ABD= TAM GIÁC AED ( C.G.C)
=>BD=BE ( 2 CẠNH TƯƠNG ỨNG)
\(\Rightarrow\widehat{ABD}=\widehat{AED}\)( 2 góc tương ứng )
b) ta có : \(\widehat{ABD}+\widehat{KBD}=180^o\left(kb\right)\)
cũng có ; \(\widehat{AED}+\widehat{CED}=180^o\left(kb\right)\)
mà \(\widehat{ABD}=\widehat{AED}\left(cmt\right)\)
=> \(\widehat{KBD}=\widehat{CED}\)
XÉT TAM GIÁC KBD VÀ TAM GIÁC CED :
\(\widehat{KBD}=\widehat{CED}\)(CMT)
BD=ED ( CMT)
\(\widehat{BDK}=\widehat{EDC}\)( ĐỐI ĐỈNH )
=> TAM GIÁC KBD = TAM GIÁC CED (G.C.G)
=>DK=DC ( 2 CẠNH TƯƠNG ỨNG)
c)
vì \(BC//KN\)(GT)
=>\(\widehat{CDN}=\widehat{DNK}\)(SO LE TRONG )
MÀ 2 GÓC NÀY LẠI Ở VỊ TRÍ SO LE TRONG CỦA KD VÀ NC
=> KD//NC
=> \(\widehat{KDN}=\widehat{CND}\)(SO LE TRONG)
XÉT TAM GIÁC KDN VÀ TAM GIÁC CND
\(\widehat{KDN}=\widehat{CND}\)( CMT)
DN-CẠNH CHUNG
\(\widehat{CDN}=\widehat{DNK}\)(CMT)
=> TAM GIÁC KDN = TAM GIÁC CND
=> KN = DC ( 2 CẠNH TƯƠNG ỨNG)
LẠI CÓ DC= DK ( CMT )
=> KN=DK
XÉT TAM GIÁC KDN:KN=DK
=> TAM GIÁC KDN CÂN TẠI K ( Đ/N)
ặc olm có cái lỗi gì ý mình gửi bài mà nó mất tỏm đi mệt quá !!!!!!! mình chẳng muốn làm lại cả bài 2 và bài 3 một tí nào !!!!!!!!!!!!!!!!

a: Xét ΔMAC có
MI là đường cao
MI là đường trung tuyến
Do đó: ΔMAC cân tại M
=>\(\widehat{AMC}=180^0-2\cdot\widehat{ACM}=180^0-2\cdot\widehat{ACB}\left(1\right)\)
ΔABC cân tại A
=>\(\widehat{BAC}=180^0-2\cdot\widehat{ACB}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{AMC}=\widehat{BAC}\)
b:
ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}\)
ΔMAC cân tại M
=>\(\widehat{MAC}=\widehat{MCA}=\widehat{ACB}\)
\(\widehat{ABM}+\widehat{ABC}=180^0\)(hai góc kề bù)
=>\(\widehat{ABM}=180^0-\widehat{ABC}=180^0-\widehat{ACB}\left(3\right)\)
\(\widehat{CAN}+\widehat{CAM}=180^0\)(hai góc kề bù)
=>\(\widehat{CAN}+\widehat{ACB}=180^0\)
=>\(\widehat{CAN}=180^0-\widehat{ACB}\left(4\right)\)
Từ (3) và (4) suy ra \(\widehat{ABM}=\widehat{CAN}\)
Xét ΔABM và ΔCAN có
AB=CA
\(\widehat{ABM}=\widehat{CAN}\)
BM=AN
Do đó;ΔABM=ΔCAN
c: ΔABM=ΔCAN
=>NC=MA
mà MA=MC
nên NC=MC
\(\widehat{AMC}=\widehat{BAC}\)
mà \(\widehat{BAC}=45^0\)
nên \(\widehat{AMC}=45^0\)
Xét ΔCMN có CM=CN và \(\widehat{CMN}=45^0\)
nên ΔCMN vuông cân tại C
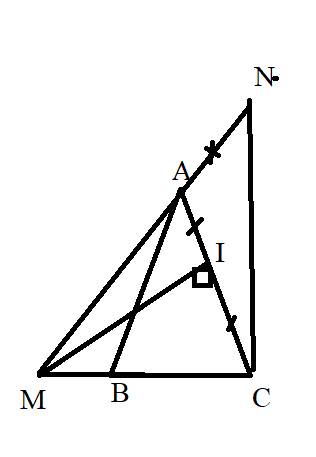
Để chứng minh điều này, ta có thể sử dụng các bước sau:
Vậy ta đã chứng minh được DH song song với AC.