Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B A C E D
\(\Delta ADC\perp A\)= > \(\widehat{ADC}+\widehat{DCA}=90^0\)
= > Góc ADC là góc nhọn
Mà \(\widehat{EDC}\)và \(\widehat{ADC}\)là 2 góc kề bù
= > \(\widehat{EDC}+\widehat{ADC}=180^0\)
\(\Rightarrow\widehat{EDC}=180^0-\widehat{ADC}\)
= > Góc EDC là góc tù
Xét \(\Delta DEC\)có góc EDC tù
= > Cạnh EC là cạnh lớn nhất trong tam giác DEC
= > EC > DC ( 1 )
\(\Delta AEC\perp A\)= > \(\widehat{AEC}+\widehat{ECA}=90^0\)
= > Góc AEC là góc nhọn
Mà \(\widehat{AEC}\)và \(\widehat{BEC}\)là 2 góc kề bù
= > \(\widehat{AEC}+\widehat{BEC}=180^0\)
\(\widehat{BEC}=180^0-\widehat{AEC}\)
= > BEC là góc tù
Xét \(\Delta BEC\)có góc BEC là góc tù
= > BC là cạnh lớn nhất trong tam giác BEC
= > BC > EC ( 2 )
Từ ( 1 ) và ( 2 ) = > BC > EC > DC

a)
+ Trong ΔABC có: góc ABC đối diện cạnh AC, góc ACB đối diện cạnh AB.
b) ΔAED có:
⇒ AE < AD hay AD > AE

(Bạn tự vẽ hình giùm)
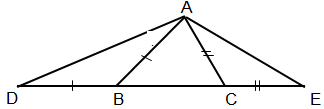
a/ Ta có AC > AB (gt) => \(\widehat{AEB}< \widehat{ADC}\)(quan hệ giữa góc và cạnh đối diện)
b/ Ta có EC < EB => AE < AB (quan hệ giữa đường xiên và hình chiếu) (1)
và CB < CD => AB < AD (quan hệ giữa đường xiên và hình chiếu) (2)
Từ (1) và (2) => AE < AD

a: Xét ΔCAD và ΔCED có
CA=CE
\(\widehat{ACD}=\widehat{ECD}\)
CD chung
Do đó: ΔCAD=ΔCED
b: Ta có:ΔCAD=ΔCED
=>\(\widehat{CAD}=\widehat{CED}\)
mà \(\widehat{CAD}=90^0\)
nên \(\widehat{CED}=90^0\)
=>DE\(\perp\)BC
c: ta có: ΔCAD=ΔCED
=>DA=DE
=>D nằm trên đường trung trực của AE(1)
ta có: CA=CE
=>C nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra CD là đường trung trực của AE
d: Ta có: ΔACD vuông tại A
=>CD là cạnh lớn nhất trong ΔACD
=>CD>DA

a.
b. Xét ΔADE có góc ADE < góc AED (chứng minh ở phần a)
=> AE < AD (Quan hệ giữa góc - cạnh đối diện trong tam giác)
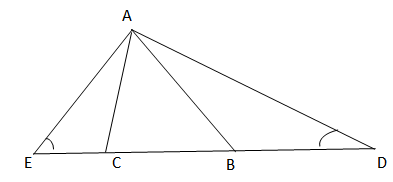
a) So sánh ˆADCADC^ và ˆAECAEC^
Ta có: AC < AB
=> ˆABC<ˆACBABC^<ACB^ (1)
Vì AC = EC => ∆AEC cân tại C
=> ˆAEC<ˆCAEAEC^<CAE^
Mà ˆACB=ˆAEC+ˆEACACB^=AEC^+EAC^ (góc ngoài tại C của ∆AEC)
=> ˆACB=2.ˆAECACB^=2.AEC^ (2)
Chứng minh tương tự : ˆABC=2ˆADCABC^=2ADC^ (3)
Từ (1), (2), (3) => 2ˆAEC=2ˆADC2AEC^=2ADC^ hay ˆAEC=ˆADCAEC^=ADC^
b) ∆AED có:
ˆAED=ˆADEAED^=ADE^ (chứng minh trên) => AD = AE

xét tam giác ABC có : AC < AB
=> góc ABC < góc ACB (đl)
góc ABC + góc ABD = 180
góc ACB + góc ACE = 180
=> góc ACE < góc ABD
có tam giác ACE và tam giác ABD lần lượt cân tại C và B
=> góc E = (180 - góc ACE) : 2 và góc D = (180 - góc ABD) : 2 (đl)
=> góc E > góc D
a)
+ Trong ΔABC có: góc ABC đối diện cạnh AC, góc ACB đối diện cạnh AB.
b) ΔAED có:
⇒ AE < AD hay AD > AE