Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
a/ Trong TG ABC vuông : AC2=BC2- AB2 (Định lý Py-ta-go đảo)
AC2=102- 62= 82
=> AC = 8 (cm)
b/ Xét 2 TG ABD và TG IBD , ta có :
BD chung
Góc ABD = Góc IBD (gt)
BA = BI (gt)
=> TG ABD = TG IBD (c-g-c)

Ai đó giúp mình với! Mình đang cần gấp!:( Các bạn vẽ hình lun giúp mình nha! Cảm ơn các bạn nhìu!:)
Do tam giác ABC có
AB = 3 , AC = 4 , BC = 5
Suy ra ta được
(3*3)+(4*4)=5*5 ( định lý pi ta go)
9 + 16 = 25
Theo định lý py ta go thì tam giác abc vuông tại A

a) Có A là hình chiếu của C trên đoạn A
CB là dường xiên của đoạn AB
Suy ra CB lớn hơn AC
Xét Tam giác ABC có
AB nhỏ hơn AC nhỏ hơn CB
Suy ra góc C nhỏ hơn góc B nhỏ hơn góc A (quan hệ giữa góc và cạnh đới diện)
b)CÓ BI là p/g (gt)
Suuy ra góc DBI = góc ABI
Xét tam giác AIB và tam giác DIB có
IB chung
góc DBI = góc ABI (cmt)
AB = BD (gt)
Suy ra tam giác BAI = tam giác BDI (cgc)
Suy ra góc BAI = góc IDB (2 góc tương ứng)
mà góc BAI = 90 độ (tam giác ABC vuông tại A)
Suy ra góc IDB = 90 độ
Suy ra ID vuông góc với BC (định nghĩa)
Đợi mình nghĩ ra câu C

a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
=>DA=DE
=>D nằm trên đường trung trực của AE(1)
ta có: BA=BE
=>B nằm trên trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE
=>BD\(\perp\)AE tại trung điểm của AE
c: Ta có: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BED}=90^0\)
=>DE\(\perp\)BC
Ta có: AH\(\perp\)BC
DE\(\perp\)BC
Do đó: AH//DE
d: Ta có: \(\widehat{EDC}+\widehat{ACB}=90^0\)(ΔEDC vuông tại E)
\(\widehat{ABC}+\widehat{ACB}=90^0\)(ΔABC vuông tại A)
Do đó: \(\widehat{EDC}=\widehat{ABC}\)
e: Xét ΔDAK vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDAK=ΔDEC
=>AK=EC và DK=DC
Ta có: BA+AK=BK
BE+EC=BC
mà BA=BE và AK=EC
nên BK=BC
=>B nằm trên đường trung trực của KC(3)
Ta có: DK=DC
=>D nằm trên đường trung trực của KC(4)
Ta có: MK=MC
=>M nằm trên đường trung trực của KC(5)
Từ (3),(4),(5) suy ra B,D,M thẳng hàng

bạn tự vẽ hình nha
a) Áp dụng định lý Pi-ta-go cho tam giác ABC vuông tại A
=> \(AB^2+AC^2=BC^2\)
\(3^2+4^2=BC^2\)
\(9+16=BC^2\)
=> \(BC^2=25\)
=>\(BC=5\)
b) Xét tam giác ABD và tam giác EBD có:
\(\widehat{BAD}=\widehat{BED}\left(=90độ\right)\)
BD chung
\(\widehat{ABD}=\widehat{EBD}\left(gt\right)\)
=> tam giác ABD = tam giác EBD (ch-gn)
c)Vì tam giác ABD = tam giác EBD
=>\(BA=BE\left(1\right)\)
Theo đề bài ta có:
\(AK=EC\left(2\right)\)
Cộng 2 vế của (1),(2)
=>\(BA+AK=BE+EC\)
\(BK=BE\)
=> tam giác BKC cân
=>\(\widehat{BKC}=\widehat{BCK}\)
d)Xét tam giác BAI và tam giác BEI có:
IB chung
\(\widehat{ABI}=\widehat{EBI}\left(gt\right)\)
\(AB=BE\)
=> tam giác BAI = tam giác BEI (c-g-c)
=>AI = EI
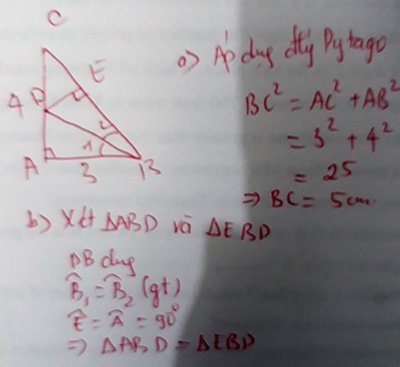
a) Tính AC
Xét tam giác ABC vuông tại A ( gt )
BC2=AB2+AC2( Py ta go)
102=62+AC2
100=36+AC2
AC2=100-36=64
AC=Căn 64=8 cm