Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có
E là trung điểm của AC
M là trung điểm của BC
Do đó: EM là đường trung bình của ΔABC
Suy ra: EM//AD và EM=AD
hay ADME là hình bình hành

\(\widehat{MDA}=1v\)( Vì MD vuông góc AB )
\(\widehat{MEA}=1v\)( vì ME vuông góc AC )
\(\widehat{BAC}=1v\)( gt )
\(\Rightarrow\)ADME - hình chữ nhật ( đpcm )

a)\(\Delta ABC\) vuông tại A nên \(\widehat{BAC}=90^o\Rightarrow\widehat{DAE}=90^o\)
Có D là hình chiếu của M trên AB \(\Rightarrow MD\perp AB\Rightarrow\widehat{MDA}=90^o\)
Có E là hình chiếu của M trên AC \(\Rightarrow ME\perp AC\Rightarrow\widehat{AEM}=90^o\)
Xét tứ giác: \(ADEM\) có \(\left\{{}\begin{matrix}\widehat{DAE}=90^o\\\widehat{MDA}=90^o\\\widehat{AEM}=90^o\end{matrix}\right.\)
\(\Rightarrow\)Tứ giác ADEM là hình chữ nhật
Vậy tứ giác ADEM là hình chữ nhật.
b)\(\Delta ABC\) vuông tại A có AM là trung tuyến (M là trung điểm BC)
\(\Rightarrow AM=\dfrac{1}{2}BC\)
Mà \(AM=DE\) (tính chất hcn)
\(\Rightarrow DE=\dfrac{1}{2}BC\left(đpcm\right)\)
Bổ sung đề: Tam giác ABC vuông tại A
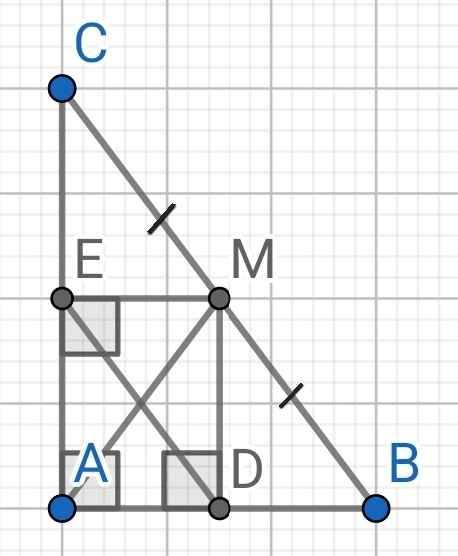 a) Xét tứ giác ADME có:
a) Xét tứ giác ADME có:
∠AEM = ∠EAD = ∠ADM = 90⁰ (gt)
⇒ ADME là hình chữ nhật
b) Do ADME là hình chữ nhật (cmt)
⇒ AM = DE (1)
Lại có:
AM là đường trung tuyến ứng với cạnh huyền BC
⇒ AM = BC/2 (2)
Từ (1) và (2) ⇒ DE = BC/2

Bài 2 :
a, Xét tam giác ABC ta có :
D là trung điểm AB
M là trung điểm CB
=)) DM là đường TB tam giác ABC
=)) DM // AC hay DM // AE (1)
Ta có : E là trung điểm AC
M là trung điểm BA
=)) EM là đường TB tam giác ABC
=)) EM // AB hay EM // AD (2)
Từ 1;2 =)) Tứ giác ADME là hình bình hành
b, Nếu tam giác ABC cân tại A => AM là đường trung tuyến AM
=)) AM đồng thời là tia phân giác của ^A
Xét hình bình hành ADME có 2 đường chéo AM là tia phân giác của ^A (cmt)
=)) Tứ giác ADME là hình thoi
c, Nếu tam giác ABC vuông tại A => ^A = 90^0
Xét hình bình hành ADME có ^A =90^0
=)) Tứ giác ADME là hình chữ nhật

2/
a/ hình thang ABCD có
AB // EF
==> AB // KF
xét tam giác ABC có
F là trung điểm của BC
AB // KF
==> KF là đường trung bình của tam giác ABC
==> K là trung điểm của AC
==> AK = KC
b/
E là trung điểm AD
F là trung điểm BC
==> EF là đường trung bình của hình thang ABCD
==> EF = (AB + CD) / 2 = (4 + 10) / 2 = 7(cm)
KF là đường trung bình của tam giác ABC nên
KF = AB / 2 = 4 / 2 = 2(cm)
==> EK = EF - KF = 7 - 2 = 5(cm)
vậy EK = 5(cm), KF = 2 (cm)
3/
a/ ta có
D là trung điểm của AB
M là trung điểm của BC
==> DM là đường trung bình của tam giác ABC
==> Dm // AC
==> DM // AE ( E thuộc AC, DM // AC)
chứng minh tương tự ta có
ME là đường trung bình của tam giác ABC
==> AD // ME
tứ giác ADME có DM // AE, AD // ME nên là HBH
b/ ( nếu tam giác ABC cân tại A)
tam giác ABC cân tại A ==> AB = AC
AD = 1/2 AB (D là trung điểm của AB)
AE = 1/2 AC (E là trung điểm của AC)
==> AD = AE
c/ (nếu tam giác ABC vuông)
ta có
tứ giác ADME là HBH
góc A = 90 độ
==> tứ giác ADME là HCN
d/ ta có
AB^2 + AC^2 = BC^2
6^2 + 8^2 = 100
==> BC = 10(cm)
AM là đường trung tuyến của tam giác ABC
==> AM = 1/2 BC = 1/2 . 10 = 5(cm)
vậy AM = 5cm
Bài 2:Cho mk ý kiến,sai đề à???4cm=6cm nhé

Bài 3:

Bài 4:
Nối D với E, nối D với M:
Chứng minh được ED//FB (BEDF là hình thoi) (1)
BF là đường trung bình tam giác AMD
=> MD//FB (tc) (2)
(1),(2) => MD trùng với ED (định lý) ( Qua 1 điểm ko thuộc đường thẳng a có 1 và chỉ 1 đường thẳng đi qua điểm đó và song song với đường thẳng a )
từ đó bạn có thể cm BMCD là hình chữ nhật ( nếu cần )
( xét từ1 giác BDCM có BC cắt DM tại trung điểm của mỗi đoạn ->BMCD là Hình chữ nhật)
Bài 5:


a) Xét ΔABC có
F là trung điểm của AC(gt)
M là trung điểm của BC(gt)
Do đó: FM là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
⇒FM//AB và \(FM=\dfrac{AB}{2}\)(Định lí 2 về đường trung bình của tam giác)
mà E∈AB và \(AE=\dfrac{AB}{2}\)(E là trung điểm của AB)
nên FM//AE và FM=AE
Xét tứ giác AEMF có
FM//AE(cmt)
FM=AE(cmt)
Do đó: AEMF là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Hình bình hành AEMF có \(\widehat{FAE}=90^0\)(ΔABC vuông tại A)
nên AEMF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
a. xét tg adme có:
mda = 90 độ
dae = 90 độ
dme = 90 độ
=> adme là hcn
b. xét tam giác abc vuông tại a có am trung tuyến => am = mc = bm
=> mca cân tại m
=> me vừa là trung tuyến + đường cao
=> e trung tuyến => ae = c = 4cm
cmt^2 => ad = db = 3cm
xét tam giác ade vuông tại e có:
ad^2 + ae^2 = de^2
3^2 + 4^2 = de^2
=> de = 5cm
vậy de = 5cm.